jonka Juan Lopez 3 vuotta sitten
347
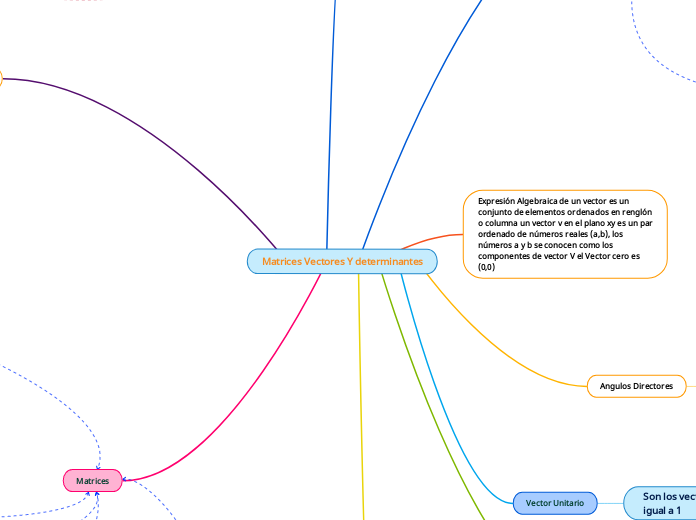
Matrices Vectores Y determinantes
En el estudio de las matemáticas, los determinantes y sistemas de ecuaciones lineales juegan un papel crucial para resolver problemas complejos de manera eficiente. Los determinantes permiten abordar la discusión y resolución de sistemas de ecuaciones mediante un procedimiento riguroso y metódico.