jonka antonella senese 4 vuotta sitten
508
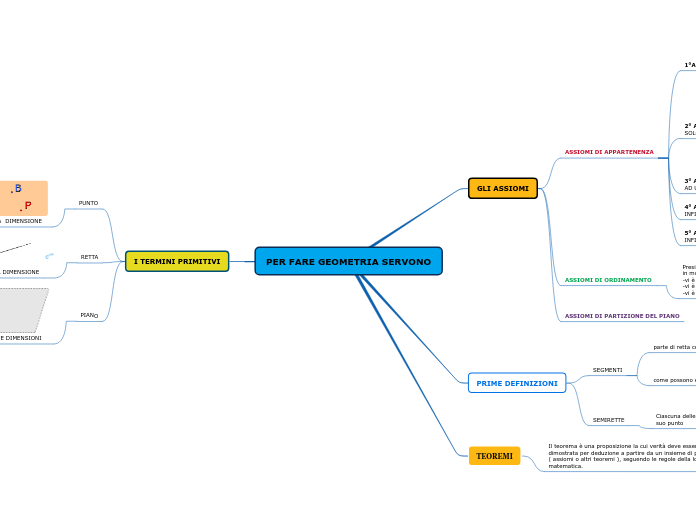
PER FARE GEOMETRIA SERVONO
La geometria si basa su teoremi e assiomi, che sono fondamentali per dimostrare proposizioni matematiche attraverso deduzioni logiche. I teoremi, derivati da assiomi o altri teoremi, richiedono rigorose dimostrazioni.