Vertex Form

Lisää tämän kaltaisia

Quadratics Concept Map Assignment

luonut Rushikesh Amin

PORIFERA

luonut tulsi N

Amorphic Design

luonut Beatriz Nava

Intervention Map

luonut Amanda Clapp

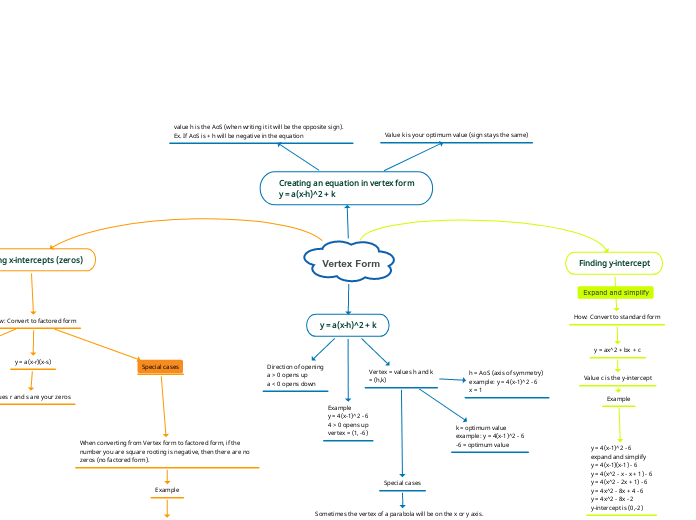
Vertex Form

Creating an equation in vertex form y = a(x-h)^2 + k

Value k is your optimum value (sign stays the same)

value h is the AoS (when writing it it will be the opposite sign). Ex. If AoS is + h will be negative in the equation

Finding y-intercept

How: Convert to standard form

y = ax^2 + bx + c

Value c is the y-intercept

y = 4(x-1)^2 - 6 expand and simplify y = 4(x-1)(x-1) - 6 y = 4(x^2 - x - x + 1) - 6 y = 4(x^2 - 2x + 1) - 6 y = 4x^2 - 8x + 4 - 6 y = 4x^2 - 8x - 2 y-intercept is (0,-2)

Finding x-intercepts (zeros)

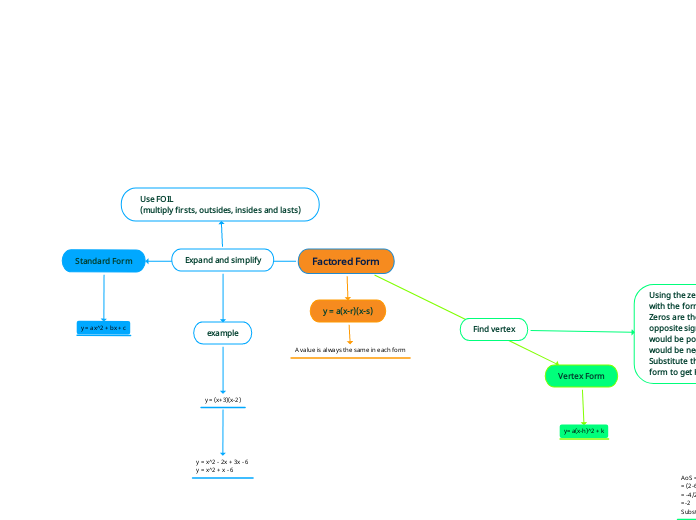
How: Convert to factored form

y = a(x-r)(x-s)

Values r and s are your zeros

When converting from Vertex form to factored form, if the number you are square rooting is negative, then there are no zeros (no factored form).

y = 2/3(x-3)^2 + 5 0 = 2/3(x-3)^2 + 5 -5 = 2/3(x-3)^2 (-5)/(2/3) = (2/3(x-3)^2)/(2/3) -7.5 = (x-3)^2 cannot square root -7.5, therefore there are no zeros

y = 4(x-1)^2 - 6 set y as 0 0 = 4(x-1)^2 - 6 move constant over to other side 6 = 4(x-1)^2 divide each side by value a 6/4 = (4(x-1)^2)/4 1.5 = (x-1)^2 sqrt each side to cancel out ^2 + or - sqrt 1.5 = sqrt (x-1)^2 solve for x +1.22 (rounded) = x-1 x = 2.22 -1.22 = x-1 x = -0.22 x-intercepts are (2.22,0) and (-0.22,0)

y = a(x-h)^2 + k

Example y = 4(x-1)^2 - 6 4 > 0 opens up vertex = (1, -6)

Vertex = values h and k = (h,k)

Special cases

Sometimes the vertex of a parabola will be on the x or y axis. This means that the x or y value of the vertex will be 0. The equation may not have either the value of -h or k

Example

y = 3(x)^2 + 3 vertex = (0,3)

k = optimum value example: y = 4(x-1)^2 - 6 -6 = optimum value

h = AoS (axis of symmetry) example: y = 4(x-1)^2 - 6 x = 1

Direction of opening a > 0 opens up a < 0 opens down