Vertex Form
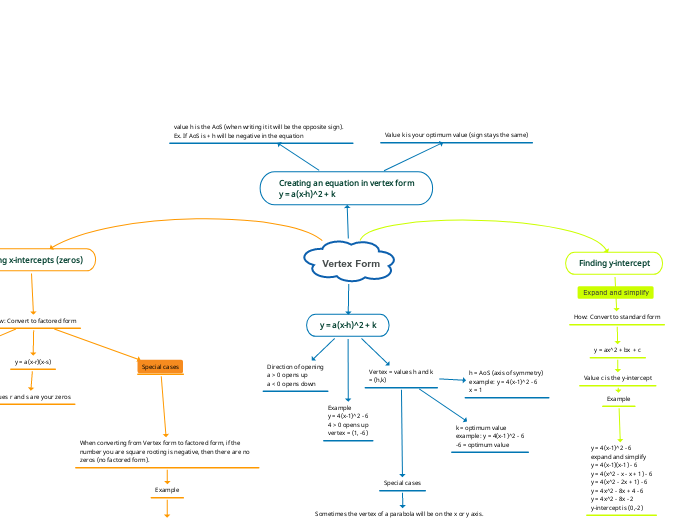
Creating an equation in vertex form
y = a(x-h)^2 + k
Value k is your optimum value (sign stays the same)
value h is the AoS (when writing it it will be the opposite sign). Ex. If AoS is + h will be negative in the equation
Finding y-intercept
How: Convert to standard form
y = ax^2 + bx + c
Value c is the y-intercept
y = 4(x-1)^2 - 6
expand and simplify
y = 4(x-1)(x-1) - 6
y = 4(x^2 - x - x + 1) - 6
y = 4(x^2 - 2x + 1) - 6
y = 4x^2 - 8x + 4 - 6
y = 4x^2 - 8x - 2
y-intercept is (0,-2)
Finding x-intercepts (zeros)
How: Convert to factored form
y = a(x-r)(x-s)
Values r and s are your zeros
When converting from Vertex form to factored form, if the number you are square rooting is negative, then there are no zeros (no factored form).
y = 2/3(x-3)^2 + 5
0 = 2/3(x-3)^2 + 5
-5 = 2/3(x-3)^2
(-5)/(2/3) = (2/3(x-3)^2)/(2/3)
-7.5 = (x-3)^2
cannot square root -7.5, therefore there are no zeros
y = 4(x-1)^2 - 6
set y as 0
0 = 4(x-1)^2 - 6
move constant over to other side
6 = 4(x-1)^2
divide each side by value a
6/4 = (4(x-1)^2)/4
1.5 = (x-1)^2
sqrt each side to cancel out ^2
+ or - sqrt 1.5 = sqrt (x-1)^2
solve for x
+1.22 (rounded) = x-1
x = 2.22
-1.22 = x-1
x = -0.22
x-intercepts are (2.22,0) and (-0.22,0)
y = a(x-h)^2 + k
Example
y = 4(x-1)^2 - 6
4 > 0 opens up
vertex = (1, -6)
Vertex = values h and k
= (h,k)
Special cases
Sometimes the vertex of a parabola will be on the x or y axis. This means that the x or y value of the vertex will be 0. The equation may not have either the value of -h or k
Example
y = 3(x)^2 + 3
vertex = (0,3)
k = optimum value
example: y = 4(x-1)^2 - 6
-6 = optimum value
h = AoS (axis of symmetry)
example: y = 4(x-1)^2 - 6
x = 1
Direction of opening
a > 0 opens up
a < 0 opens down