Álgebra Lineal I

Plus de détails

¿QUE SON LOS ELEMENTOS MAYORES Y MENORES?

par DIANA ESPERANZA MANOPANTA QUILUMBA

EXPRESION ALGEBRAICA DE UN VECTOR : Es un conjunto de elementos ordenados en renglón o columna. Un vector v en el plano xy es un par ordenado de números reales (a,b). Los números a y b se conocen como las componentes del vector v. El vector cero es (0,0).

par Deisy Yolanda Amortegui Sanchez

MITOCONDRIAS Y RESPIRACIÓN CELULAR

par angela julieth reyes garcia

MAPA CONCEPTUAL ADMINISTRACION

par jenifer espitia

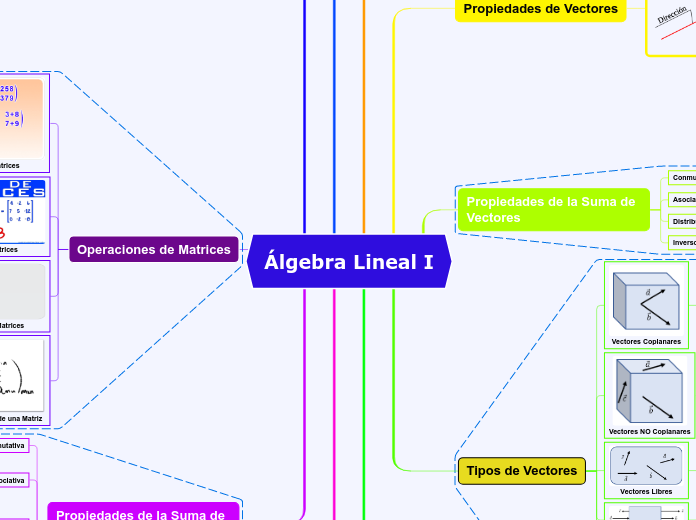
Álgebra Lineal I

The part of speech is a category to which a word is assigned according to its syntactic functions. In English the main parts of speech are noun, pronoun, adjective, determiner, verb, adverb, preposition, conjunction, and interjection.

TIPOS DE MATRICES

An article is a word used to modify a noun, which is a person, place, object, or idea. Technically, an article is an adjective, which is any word that modifies a noun.

Matriz Identidad

Es de orden n x n, solo tiene 1 en la diagonal principal, y el resto son ceros.

Matriz Triangular

Solo tiene elementos por encima o por debajo de la diagonal principal.

Matriz Escalar

Matriz Diagonal con los elementos de la diagonal principal todos iguales.

Matriz Diagonal

Es una matriz n x n que solo tiene elementos en la diagonal principal, y el resto son ceros.

Matriz Fila

Matrices con una sola fila.

Matriz Columna

Matrices con una sola columna.

Matriz Rectangular

Son matrices de orden m x n con m distinto de n

Indefinite article

Indefinite articles are the words 'a' and 'an.' Each of these articles is used to refer to a noun, but the noun being referred to is not a specific person, place, object, or idea. It can be any noun from a group of nouns.

A car in the parking lot.

Definite article

It refers directly to a specific noun or groups of nouns.

Create sentences

The breakfast on my plate.

Matriz Cuadrada

Son matrices de orden n x n

Propiedades de la Suma de Matrices

Módulo del Producto

1A=A

Módulo de la Suma

A+O=O+A=A

A+(-A)=(-A)+A=0

(k+m)A=kA+mA

k(mA)=km(A)

Operaciones de Matrices

Producto de un escalar de una Matriz

Se multiplica cada elemento de la matriz por el escalar.

Multiplicación de Matrices

Se realiza entre una matriz m x n y otra n x m, multiplicando filas por columnas y sumando.

Resta de Matrices

Se realiza con matrices del mismo orden, restando uno a uno sus componentes.

Suma de Matrices

Se hace con matrices del mismo orden, sumando cada elemento respectivo.

Propiedades de Matrices

Determinante 2x2

Determinantes n x n

Determinante nxn

Determinante

Es un número asociado a la matriz, y que nos permite saber propiedades que puede cumplir dicha matriz.

Elementos de una Matriz

Elementos de la matriz

Se denotan por subindices aij donde la i es el numero de fila, y la j el numero de columna.

Orden de la matriz

El orden se denota por m x n donde m son las filas y n las columnas.

Columna de una matriz

Lineas verticales de una matriz.

Filas de una matriz

Lineas horizontales de la matriz.

Operaciones de Vectores

A conjunction is a word like 'if' 'but' or 'and' which is used to connect sentences or clauses together.

Producto Vectorial

El resultado del producto cruz es un tercer vector perpendicular a los dos primeros.

Producto Punto

El producto de dos vectores, no da otro vector, sino un escalar.

Resta de Vectores

Se realiza con la forma negativa del vector que se resta.

Producto por un escalar

Subordinating conjunctions are conjunctions that are used at the beginning of subordinate clauses. Some examples of these conjunctions are: although, after, before, because, how, if, once, since, so that, until, unless, when etc.

Puede multiplicarse un vector por un escalar positivo o negativo.

Suma de Vectores

Coordinating conjunctions always connect phrases, words, and clauses. They are: for, and, nor, but, or, yet, so.

Se realiza gráficamente o algebraicamente.

Tipos de Vectores

An adjective is a word that's used to describe a specific noun and to provide more detail to the listener.

Vectores BASE

Dos vectores con distinta dirección forman una base. Cualquier vector del plano que forman puede hallarse como composicion lineal de estos.

Vectores Concurrentes o Angulares

Se cruzan en algún punto sobre la misma dirección o línea de acción. Forman un ángulo entre ellos.

Se encuentran en la misma dirección o línea de acción.

Vectores Libres

No poseen un punto de aplicación en particular.

Vectores NO Coplanares

Superlative adjectives demonstrate a higher level of comparison between entities.

NO están en el mismo plano.

Vectores Coplanares

Expresses a comparison between two entities or groups of entities in quality or degree.

Están sobre el mismo plano.

Propiedades de la Suma de Vectores

A preposition is one of the most exciting parts of grammar. A preposition is used to describe the location of something in relation to something else.

Inverso Aditivo

Participle preposition consists of words that end in “ing”.

A+(-A)=0

Distributiva

When a preposition consists of more than one word, it is called double preposition.

k(A+B)=kA+kB

Asociativa

Compound preposition consists of two or more words.

(A+B)+C=A+(B+C)

Conmutativa

When a preposition consists of one word it is called single or simple preposition.

A+B=B+A

Propiedades de Vectores

A noun is defined as a person, place, thing or idea. Proper nouns always begin with a capital letter. Common nouns, which are general words, such as 'cars,' are not capitalized.

Propiedades

Igualdad de dos vectores

Dos vectores son iguales cuando coinciden en magnitud, dirección y sentido.

Sentido

Es determinado por la flecha en la que termina.

Módulo o Magnitud

Es la longitud del vector

Dirección

Es la recta que lo contiene o una de sus paralelas.

Origen o Punto de Aplicación

Es el punto exacto donde actúa el vector.

Elementos de un Vector

A verb is an action word or 'doing' word that signifies movement in some way.

Ángulos Directores

Son los àngulos α, β y γ que forma el ángulos en las coordenadas i,j y k respectivamente.

Vector Unitario

Es un vector de Magnitud 1

Dirección de un Vector

Se refiere al ángulo que forma el vector con el eje x

Magnitud de un Vector

Es la medida del vector, y se halla usando Pitágoras.

Expresión Algebraica de un Vector

Countable nouns are nouns that can be counted, even if the number might be extraordinarily high.

Uncountable nouns are nouns that come in a state or quantity which is impossible to count; liquids are uncountable, as are things which act
like liquids.

Es la coordenada (a,b) que identifica al vector.