par Wesley Santiago Il y a 3 années
1257
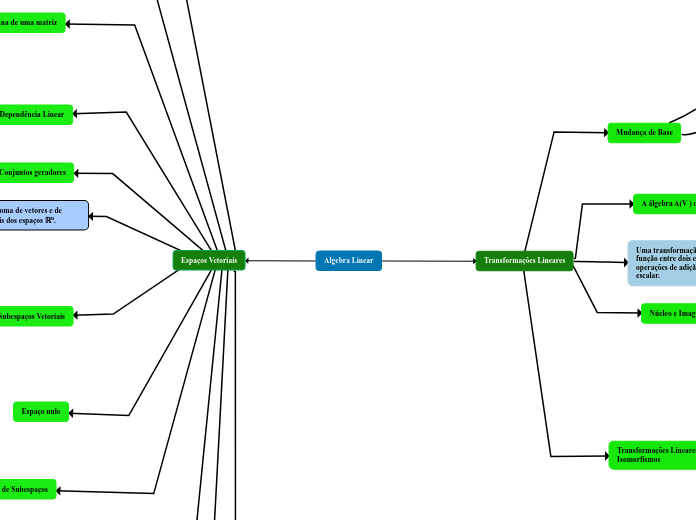
Algebra Linear
No contexto das transformações lineares, uma função que mapeia entre dois espaços vetoriais preservando adição e multiplicação por escalar é analisada. O núcleo da transformação, um subconjunto do domínio onde a função resulta no vetor nulo, e a imagem, que abrange todos os vetores resultantes, são conceitos fundamentais.