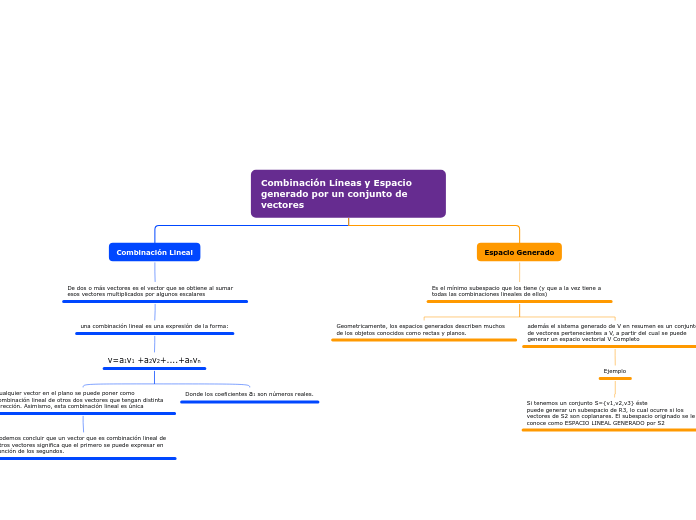
Combinación Líneas y Espacio generado por un conjunto de vectores

Plus de détails

Fuerza y Combinación De Fuerzas

par Oskle Vasquez

cantidades escalares y vectoriales

par allan hanna

Las fuerzas

par Vicente Villalobos B.

Organigrama

par Maria Jose Biendicho

Combinación Líneas y Espacio generado por un conjunto de vectores

Espacio Generado

Es el mínimo subespacio que los tiene (y que a la vez tiene a todas las combinaciones lineales de ellos)

además el sistema generado de V en resumen es un conjunto de vectores pertenecientes a V, a partir del cual se puede generar un espacio vectorial V Completo

Ejemplo

Si tenemos un conjunto S={v1,v2,v3} éste puede generar un subespacio de R3, lo cual ocurre si los vectores de S2 son coplanares. El subespacio originado se le conoce como ESPACIO LINEAL GENERADO por S2

Geometricamente, los espacios generados describen muchos de los objetos conocidos como rectas y planos.

Combinación Lineal

De dos o más vectores es el vector que se obtiene al sumar esos vectores multiplicados por algunos escalares

una combinación lineal es una expresión de la forma:

v=a1v1 +a2v2+....+anvn

Donde los coeficientes a1 son números reales.

Cualquier vector en el plano se puede poner como combinación lineal de otros dos vectores que tengan distinta dirección. Asimismo, esta combinación lineal es única

podemos concluir que un vector que es combinación lineal de otros vectores significa que el primero se puede expresar en función de los segundos.