by julian tobon 2 years ago
215
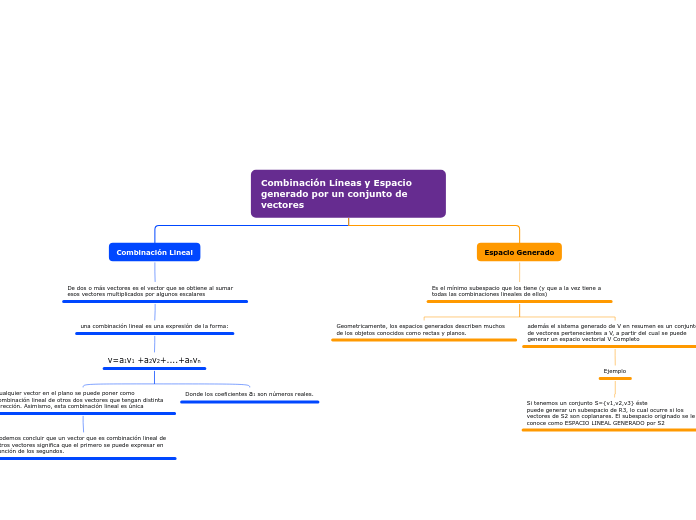
Combinación Líneas y Espacio generado por un conjunto de vectores
Un subespacio vectorial es el conjunto más pequeño que contiene a un grupo de vectores junto con todas sus combinaciones lineales. Geométricamente, estos subespacios pueden representar rectas y planos en el espacio.