par Mélina Sd Il y a 5 années
533
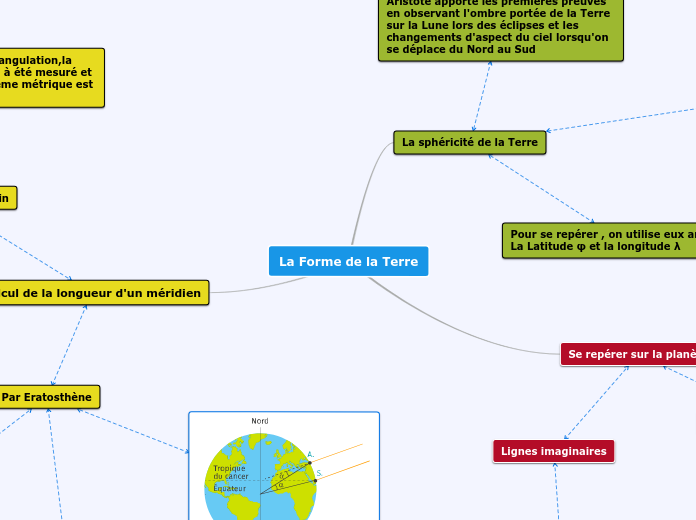
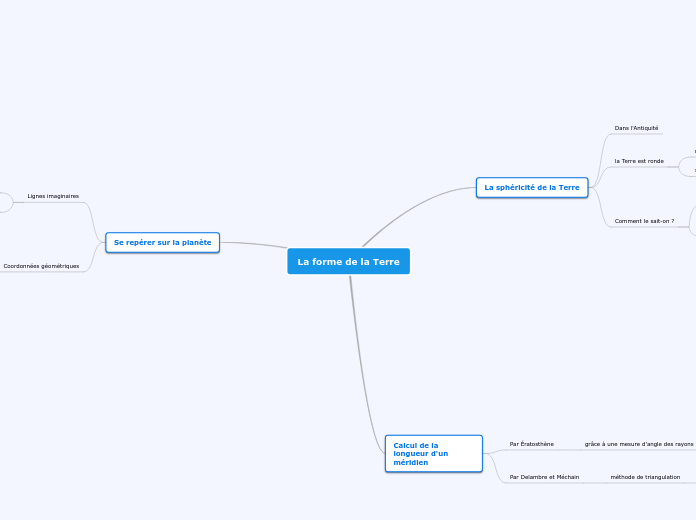
La Forme de la Terre
L'étude de la forme de la Terre et des moyens de se repérer sur celle-ci repose sur des concepts géométriques et historiques. Pythagore a introduit l'idée de la sphéricité de la Terre, et Aristote a fourni des preuves en observant l'