par Yasmith Aviles Il y a 2 années
148
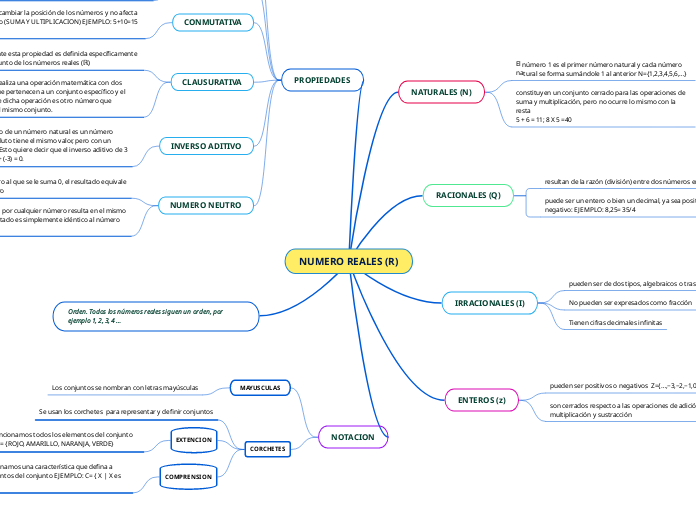
NUMERO REALES (R)
Los números reales comprenden tanto positivos como negativos y se representan con números enteros, racionales e irracionales. Los enteros, por ejemplo, forman un conjunto cerrado bajo operaciones como adición, multiplicación y sustracción.