a gxdErick gxdErick 4 éve
502
Organigrama
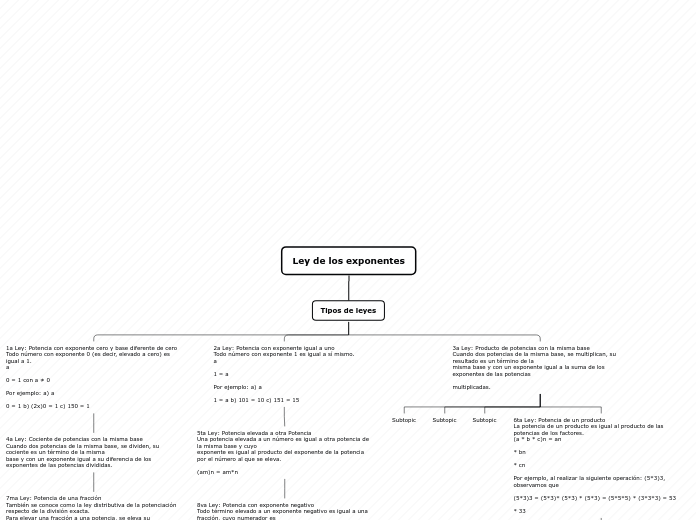
Las leyes de los exponentes son fundamentales en las matemáticas y detallan cómo manipular números elevados a potencias. Una de las reglas establece que cualquier número elevado a la potencia de cero es igual a uno, siempre que la base no sea cero.