a Daniel Temoltzin 9 éve
2772
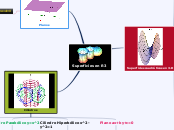
superficies en r3
En las matemáticas y la geometría, se estudian diversas superficies en el espacio tridimensional (R3). Entre las superficies más comunes se encuentran los cilindros, que pueden ser circulares, hiperbólicos o parabólicos, dependiendo de la ecuación que los define.