a jose canche 3 éve
244
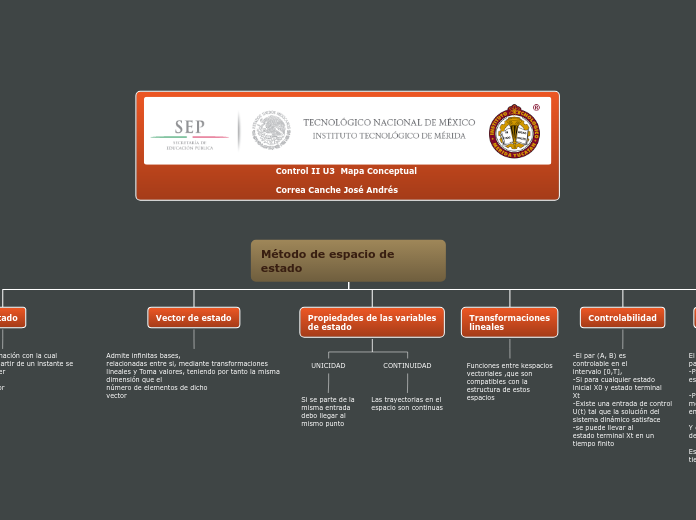
U3_CONTROL2_Correa_Canche_Jose
En el estudio de sistemas dinámicos, el concepto de estado se refiere a la mínima cantidad de información necesaria para predecir el comportamiento futuro del sistema a partir de un momento dado.