Правильні многогранники
Правильним многогранником є многогранник, грані якого є правильними многокутниками з рівною кількістю сторін, а в кожній вершині многогранника сходиться однакова кількість ребер.
Гексаедр
У куба всі шість граней – квадрати. Кожна з вершин куба є вершиною трьох квадратів. Сума плоских кутів при кожній з вершин куба дорівнює двомстам сімдесяти градусам. Куб має один центр симетрії.
- У куб можна вписати тетраедр двома способами, притому чотири вершини тетраедра будуть суміщено з чотирма вершинами куба. Всі шість ребер тетраедра лежатимуть на всіх шести гранях куба і дорівнюватимуть діагоналі грані-квадрата.
- Чотири перетини куба є правильними шестикутниками — ці перетини проходять через центр куба перпендикулярно чотирьом його діагоналям.
- У куб можна вписати октаедр, притому всі шість вершин октаедра будуть суміщено з центрами шести граней куба.
- Куб можна вписати в октаедр, притому всі вісім вершин куба будуть розташовано в центрах восьми гранях октаедра.
- У куб можна вписати ікосаедр, при цьому, шість взаємно паралельних ребер ікосаедра будуть розташовані відповідно на шести гранях куба, решта 24 ребра всередині куба, всі дванадцять вершин ікосаедра лежатимуть на шести гранях куба.
Для куба, довжина ребер якого дорівнює a:
Площа поверхні 
Діагональ грані 
Радіус описаної сфери 
Радіус вписаної сфери 
Об'єм 
Просторова діагональ 
Радіус сфери, що дотична до ребер 
Кут між гранями (у радіанах) 
Тетраедр
У правильного тетраедра всі чотири грані – рівносторонні трикутники. Кожна з його вершин є вершиною трьох трикутників. Сума плоских кутів при кожній із вершин дорівнює 180 градусам. Правильний тетраедр не має центра симетрії.
- В правильний тетраедр можна вписати октаедр, притому чотири (з восьми) грані октаедра будуть суміщено з чотирма гранями тетраедра, всі шість вершин октаедра будуть суміщено з центрами шести ребер тетраедра.
- Правильний тетраедр з ребром х складається з одного вписаного октаедра (у центрі) з ребром х/2 і чотирьох тетраедрів (по вершинам) з ребром х/2.
- Правильний тетраедр можна вписати в куб двома способами, притому чотири вершини тетраедра будуть суміщено з чотирма вершинамі куба. Всі шість ребер тетраедра лежатимуть на всіх шести гранях куба і дорівнюватимуть діагоналі грані-квадрата.
- Правильний тетраедр можна вписати в ікосаедр, притому, чотири вершини тетраедра будуть суміщено з чотирма вершинамі ікосаедра.
У правильного тетраедра з довжиною ребра a:
Площа поверхні 
Об'єм 
Висота 
Радіус вписаної сфери 
Радіус описаної сфери 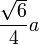
Кут нахилу ребра 
Кут нахилу грані 
Октаедр
У правильного октаедра всі вісім граней – рівносторонні трикутники. Кожна вершина октаедра є вершиною чотирьох трикутників. Сума кутів плоских кутів при кожній вершині дорівнює двомстам сорока градусам. Правильний октаедр має центр симетрії.
- Октаедр можна вписати в тетраедр, притому чотири (з восьми) граней октаедра будуть суміщено з чотирма гранями тетраедра, всі шість вершин октаедра будуть суміщено з центрами шести ребер тетраедра.
- Октаедр з ребром у складається з 6 октаедрів (по вершинам) з ребром у:2 і 8 тетраедрів (по гранях) з ребром у:2
- Октаедр можна вписати в куб, притому всі шість вершин октаедра будуть суміщено з центрами шести граней куба.
- У октаедр можна вписати куб, притому всі вісім вершин куба будуть розташовано в центрах восьми гранях октаедра.
Площа S і об'єм V октаедра з довжиною ребра а обчислюється за формулами:


Ікосаедр
У правильного ікосаедра всі двадцять граней – рівносторонні трикутники. Кожна з вершин ікосаедра є вершиною п’яти трикутників. Сума плоских кутів при кожній з вершин ікосаедра дорівнює трьомстам градусам. Правильний ікосаедр має центр симетрії.
- Ікосаедр можна вписати в куб, при цьому його шість взаємно паралельних ребер розташовуватимуться відповідно на шести гранях куба, решта 24 ребра - усередині куба, а усі дванадцять вершин ікосаедра лежатимуть на шести гранях куба.
- В ікосаедр може бути вписаний тетраедр, притому чотири вершини тетраедра будуть суміщені з чотирма вершинами ікосаедра.
- Ікосаедр можна вписати в додекаедр, притому вершини ікосаедра будуть суміщені з центрами граней додекаедра.
- У ікосаедр можна вписати додекаедр, притому вершини додекаедра будуть суміщені з центрами граней ікосаедра.
Площа S, об'єм V ікосаедра з довжиною ребра a, а також радіуси вписаної і описаної куль обчислюються за формулами:




Додекаедр
У правильного додекаедра всі дванадцять граней – правильні п’ятикутники. Кожна з вершин додекаедра є вершиною трьох правильних п’ятикутників. Сума плоских кутів при кожній з вершин дорівнює трьомстам двадцяти чотирьом градусам. Правильний додекаедр має центр симетрії.
Розгортка
Властивості
- Усі двадцять вершин додекаедра лежать по п'ять у чотирьох паралельних площинах, утворюючи в кожній з них правильний п'ятикутник.
- Двогранний кут між будь-якими двома суміжними гранями додекаедра дорівнює arccos (-1 / √5) ≈116 °, 565.
- Сума плоских кутів при кожній з 20 вершин дорівнює 324 °, тригранний кут дорівнює arccos (-11 / 5√5) ≈2,9617 стерадіан.
- У додекаедр можна вписати куб так, що сторони куба будуть діагоналями додекаедра.
- Додекаедр має три зірчасті форми.
Формули
Площа поверхні A і об'єм V додекаедра зі стороною a можна обчислити за формулами:


Радіус описаної сфери:
 , де
, де  - золотий перетин.
- золотий перетин.
Радіус вписаної сфери:

Двогранний кут між гранями:
 , де
, де  - золотий перетин.
- золотий перетин.













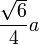










 , де
, де  - золотий перетин.
- золотий перетин.
 , де
, де 


