da Shelbi Menzie mancano 11 anni
410
Chapter 7 and 8
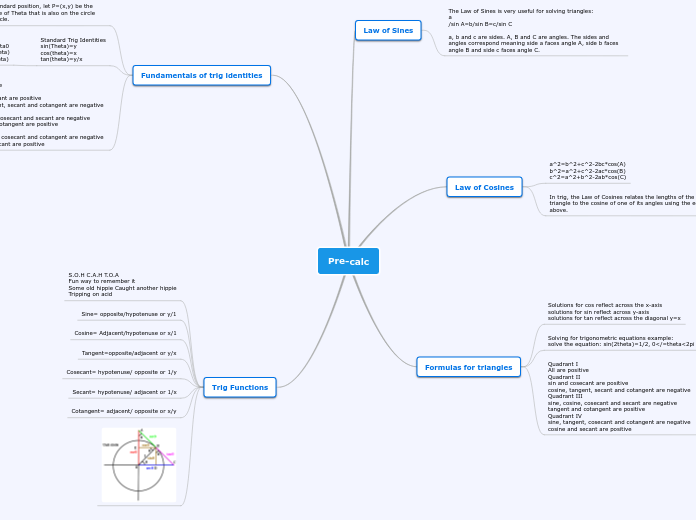
Trig functions such as cosine and sine have specific properties and behaviors that are essential in mathematics. The cosine function is defined for all real numbers and has a range between -1 and 1.