Conjunto de los Números

Più simili a questo

DESASTRES

da saby alcon

MATERIAL PARA SUTURA

da Cindy Faysuly Perilla Moreno

PRODUCTO TECNOLOGICO

da MILLARAY CARRILLO MANSILLA

CLASIFICACIÓN DE LOS NÚMEROS REALES

da Mery Perez

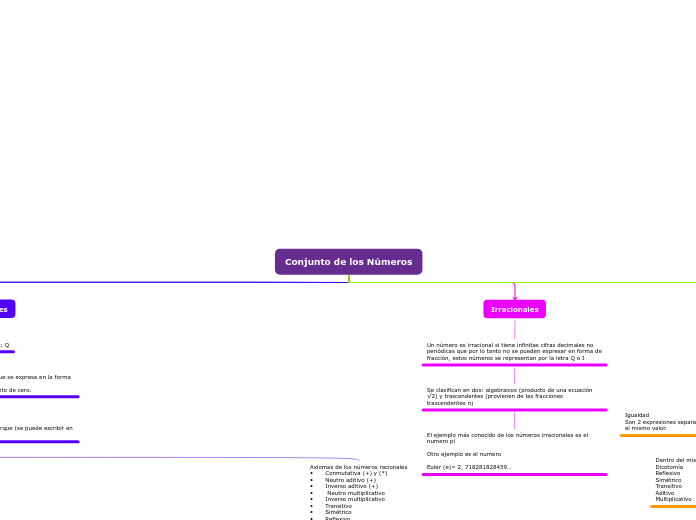
Conjunto de los Números

Enteros

Representados por la letra Z.

Formados por enteros positivos, enteros negativos y el cero.

Enteros Positivos Z+ son números mayores que cero. Ejemplo: 6,9,10

Enteros negativos Z- son números menores que cero. Ejemplo: -8,-9,-16

Enteros opuestos: números situados a la misma distancia del cero pero en sentido contrario.

Ley de signos: + por + = + + por - = - - por + = - - por - = +

Valor absoluto: es un número entero con signo positivo. Ejemplo: (-3) = 3

Axiomas de los Números Enteros

De igualdad = De la Adición + De la multiplicación x Destributivo-Recolectivo De orden < >

Naturales

Se representa con la letra N en mayúscula.

Ejemplo En una caja de dulces surtidos encontramos 9 chupetes 10 chicles 5 caramelos 20 chocolates total 44 golosinas

Es un conjunto de números que utilizamos en la vida diaria sirven para ordenar y contar.

Los números naturales se dividen en axiomas:

Distributivo Recolectivo El producto de un numero natural sumado un numero natural cualquiera es igual al producto sumado de las mismas.

Multiplicación Es cuando un numero natural a por b nos da igual un c.

Dentro de este axioma también encontramos: Clausurativo Conmutativo Asociativo Modulativo

Adición o suma Es cuando un numero natural a mas un b dan igual un numero c Dentro del mismo axioma de adición.

Encontramos: Clausurativo Conmutativo Asociativo Modulativo

Igualdad Son 2 expresiones separadas por el signo igual ambas tienen el mismo valor.

Dentro del mismo axioma encontramos: Dicotomía Reflexivo Simétrico Transitivo Aditivo Multiplicativo

Irracionales

Un número es irracional si tiene infinitas cifras decimales no periódicas que por lo tanto no se pueden expresar en forma de fracción, estos números se representan por la letra Q o I

Se clasifican en dos: algebraicos (producto de una ecuación √2) y trascendentes (provienen de las fracciones trascendentes π)

El ejemplo más conocido de los números irracionales es el numero pi Otro ejemplo es el numero Euler (e)= 2, 718281828459…

Racionales

SIMBOLOGIA: Q

Un número racional es un número que se expresa en la forma p/q donde p y q son enteros y q es distinto de cero.

Ejemplo 1,5 = 3/2 es un número racional porque (se puede escribir en forma de fracción)

Axiomas de los números racionales • Conmutativa (+) y (*) • Neutro aditivo (+) • Inverso aditivo (+) • Neutro multiplicativo • Inverso multiplicativo • Transitivo • Simétrico • Reflexivo • Dicotomía • Clausurativo • Asociativo • Modulativo

Clases de números fraccionarios • Fracción propia • Fracción impropia • Fracción mixta

Tipos números decimales

Racional Exacto Aquellos números fraccionarios que al ser dividos dejan un resto de cero Ejemplo 12/4 = 3

Racionales Periódicos Mixtos Son aquellos números que se repiten después de la coma de forma infinita y no periódica Ejemplo: 7/15= 0.466...

Racionales periódicos: son aquellos números que tienen un número ilimitado de cifras que tienen un patrón que se repite de manera cíclica. Ejemplo: 1/3= 0. 333...

Racionales finitos: Son aquellos que tienen un número limitado de cifras. Ejemplo: 1/2 = 0.25

Reales

Radicación

La radicación es el proceso de hallar raíces de orden n de un número a.

Las operaciones de la radicación son: La raíz Enésima exacta Raíz Enésima de 1(índice n, exponente m) Raíz y Potencia Enésima Raíz Enésima Inexacta

Teoremas de la Potenciación

La potenciación es una operación matemática, entre una base y un exponente, donde el exponente nos indica el número de veces que debe multiplicarse la base, para obtener un resultado llamado potencia. En nuestro ejemplo se lee: "dos tercios elevado al exponente 3" o "dos tercios al cubo".

Teoremas de la Potenciación: • Potencia Enésima positiva par • Potencia Enésima positiva Impar • Potencia Enésima del producto • Potencia Enésima del cociente

Operaciones de la Potenciación

Las operaciones de la potenciación consisten en una serie de productos de un mismo número; de la radicación que es la inversa de la potenciación y del cálculo con logaritmos, en los que el valor buscado es el exponente de una potencia. Las operaciones de poteciación son: Producto de potencias Cociente de potencias Potencia de Potencia

Se representan por la letra R.

Está formado por la unión de racionales e irracionales.

Son todos los números encontrados más frecuentes no se encuentran de manera accidental.

Axiomas de números reales

Adicción de números reales: 1. Clausurativo 2. Conmutativo 3. Asociativo 4. Modulativo 5. Invertido

1. Dicotomía 2. Reflexivo 3. Simétrico 4. Transitivo 5. Aditivo 6. Multiplicativo

Valor Absoluto El valor absoluto de un real es el mismo número con signo positivo. Se denota mediante las barras verticales.