da Mayely Cuba Fernàndez mancano 10 mesi
114
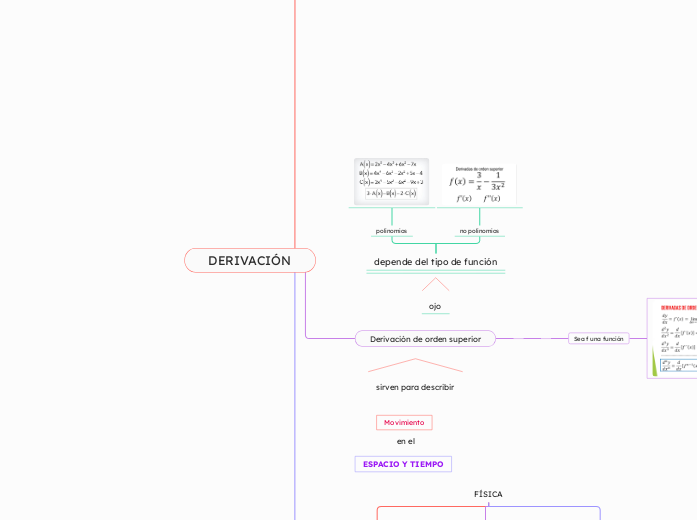
DERIVACIÓN
La derivación es un concepto fundamental en el cálculo, crucial para comprender cómo cambian las funciones. La regla de la cadena, atribuida a Leibniz, es esencial para derivar funciones compuestas.