da césar aaron mancano 4 anni
599
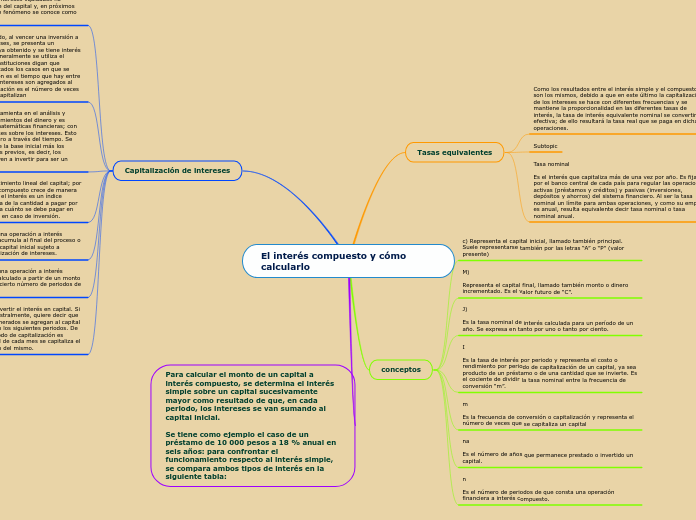
El interés compuesto y cómo calcularlo
El interés compuesto se diferencia del interés simple en que los intereses generados se reinvierten, creando así más intereses en futuros periodos. Las tasas de interés se dividen en nominales y efectivas.