da Lina Zamira Huacachi Caso mancano 2 anni
155
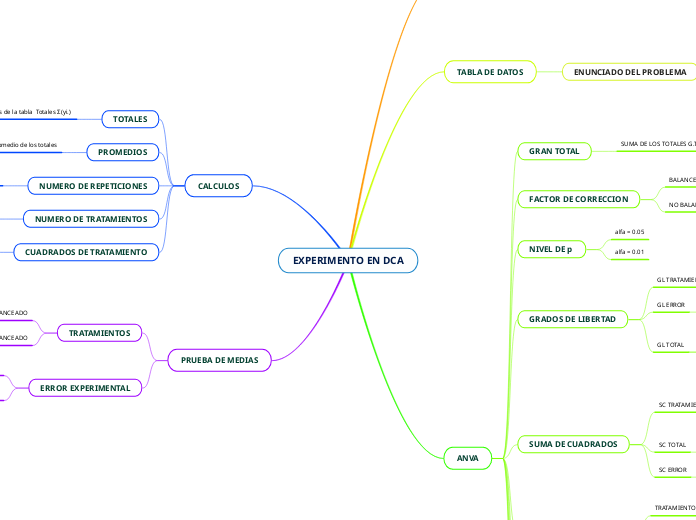
EXPERIMENTO EN DCA
El análisis de varianza (ANOVA) es una técnica estadística utilizada para comparar las medias de diferentes grupos y determinar si existen diferencias significativas entre ellos. En el diseño completamente al azar (