FUNCIONES CUADRÁTICAS
Detalles de cada sección y subsección
Las funciones cuadráticas se utilizan en la ciencia y la economía para modelar fenómenos y tomar decisiones basadas en los resultados de los modelos
Las funciones cuadráticas se utilizan para modelar la trayectoria de objetos en movimiento bajo la influencia de la gravedad u otras fuerzas
Las funciones cuadráticas se utilizan para resolver problemas donde se busca maximizar o minimizar una variable
la parábola tiene concavidad hacia abajo
la parábola tiene concavidad hacia arriba
La concavidad de una parábola depende del valor del coeficiente a
Si a < 0
el vértice representa el máximo de la función
Si a > 0
el vértice representa el mínimo de la función
El máximo o mínimo de una función cuadrática se encuentra en el vértice de la parábola
El rango de una función cuadrática depende del coeficiente a y la concavidad de la parábola
El dominio de una función cuadrática es el conjunto de todos los valores de x para los cuales la función está definida
Se obtiene expandiendo la forma vértice de la función
La forma canónica de una función cuadrática es f(x) = a(x - p)^2 + q
q) representa las coordenadas del vértice
donde (p
Se obtiene factorizando la función cuadrática
La forma factorizada de una función cuadrática es f(x) = a(x - r1)(x - r2)
donde r1 y r2 son las raíces de la función
Se obtiene completando el cuadrado en la forma general de la función
La forma vértice de una función cuadrática es f(x) = a(x - h)^2 + k
k) representa las coordenadas del vértice
donde (h
La parábola puede intersectar el eje y en el punto c
donde c es el término independiente de la función
La parábola puede intersectar el eje x en uno o dos puntos
Se calcula utilizando la fórmula x = -b / (2a) y luego sustituyendo este valor en la función para encontrar el valor de y
El vértice de una parábola es el punto más bajo o más alto de la parábola
Se calcula utilizando la fórmula x = -b / (2a)
El eje de simetría de una parábola es una línea vertical que divide la parábola en dos partes simétricas
Ejemplo 2
g(x) = -x^2 + 4x + 2
Ejemplo 1
f(x) = 2x^2 + 3x - 1
La variable x representa el dominio de la función y f(x) representa el codominio
La forma general de una función cuadrática es f(x) = ax^2 + bx + c
Su forma general es f(x) = ax^2 + bx + c
b y c son constantes
donde a
Una función cuadrática es una función polinómica de segundo grado
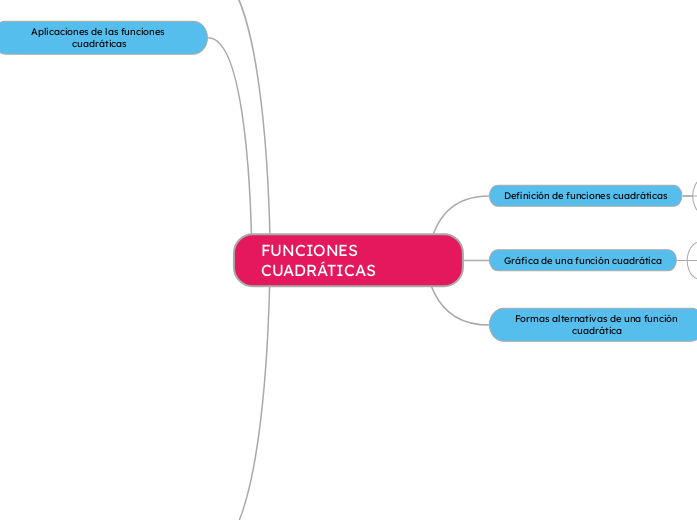
Aplicaciones de las funciones cuadráticas
Modelos matemáticos en ciencias y economía
Problemas de trayectoria de objetos en movimiento
Problemas de maximización y minimización
Propiedades de las funciones cuadráticas
Concavidad
Máximo y mínimo
Dominio y rango
Formas alternativas de una función cuadrática
Forma canónica
Forma factorizada
Forma vértice
Gráfica de una función cuadrática
Intersecciones de la parábola con los ejes
Vértice de la parábola
Eje de simetría
Definición de funciones cuadráticas
Ejemplos de funciones cuadráticas
Forma general de una función cuadrática
Explicación de una función cuadrática