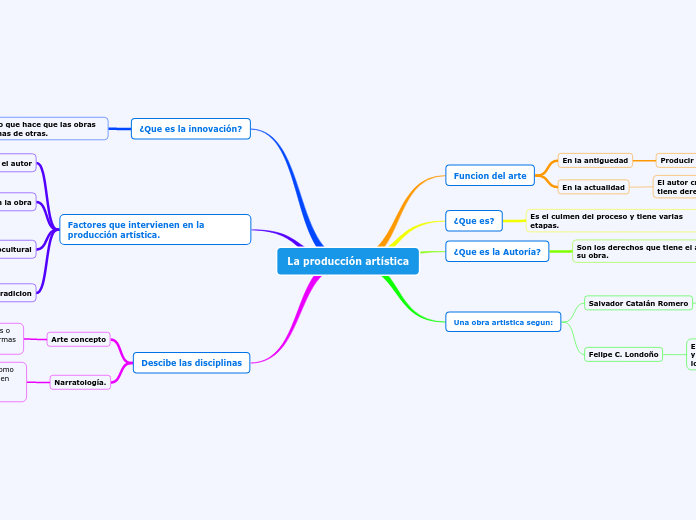
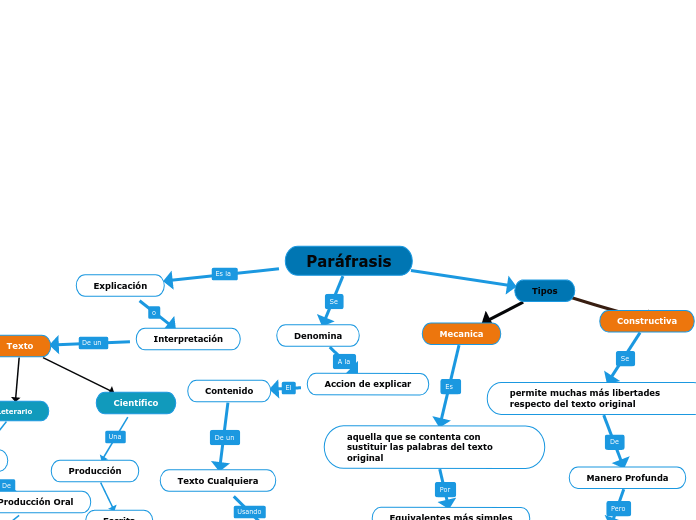
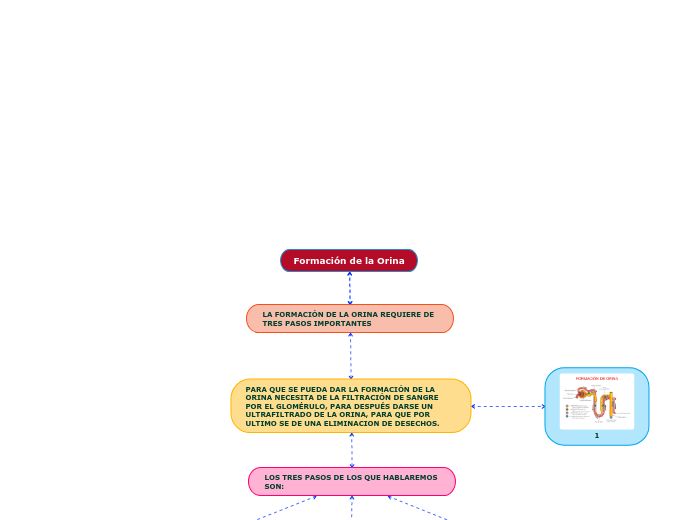
da edison david mancano 7 anni
213
presentacion de investigacion operativa
En el contexto empresarial, la implementación de modelos de programación lineal y de transporte se presenta como una herramienta esencial para la toma de decisiones. Estos métodos permiten optimizar recursos y maximizar ganancias.