によって roman lewis 3年前.
189
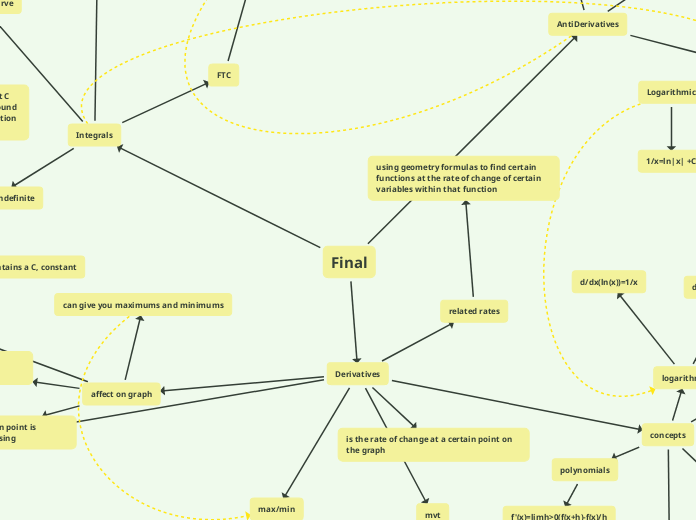
Final
The text delves into the distinctions between definite and indefinite integrals, emphasizing that definite integrals yield an exact constant based on specific points on a function, while indefinite integrals include a constant term (