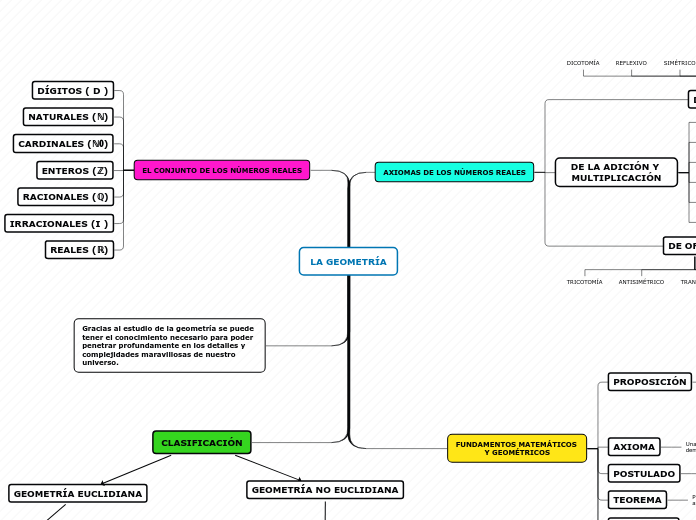
LA GEOMETRÍA
CLASIFICACIÓN
GEOMETRÍA NO EUCLIDIANA
Geometría cuyos postulados y propiedades difieren en el quinto postulado establecido por Euclides.
MOLECULAR
DIFERENCIAL
HIPERBÓLICA
GEOMETRÍA EUCLIDIANA
Estudia las propiedades del plano y del espacio tridimensional en función de los postulados de Euclides.
ANALÍTICA ESPACIAL
ANALÍTICA PLANA
ANALÍTICA
ESPACIAL
PLANA
Gracias al estudio de la geometría se puede tener el conocimiento necesario para poder penetrar profundamente en los detalles y complejidades maravillosas de nuestro universo.
EL CONJUNTO DE LOS NÚMEROS REALES
REALES (ℝ)
IRRACIONALES (I )
RACIONALES (ℚ)
ENTEROS (ℤ)
CARDINALES (ℕ𝟎)
NATURALES (ℕ)
DÍGITOS ( D )
FUNDAMENTOS MATEMÁTICOS Y GEOMÉTRICOS
PROBLEMA
Proposiciones que parte de ciertos datos hasta llegar a ciertos resultados.
COROLARIO
Proposición que es consecuencia directa de un teorema
TEOREMA
Proposición que es necesario demostrar utilizando definiciones, axiomas o postulados.
POSTULADO
Proposición que, aunque no tiene la evidencia del axioma se admite sin demostración.
AXIOMA
Una proposición que siendo evidente no requiere demostración.
PROPOSICIÓN
Es un enunciado cuyo valor de verdad no se conoce
COMPUESTAS
OPERADORES LÓGICOS
Son símbolos de relación que afectan a las proposiciones simples.
SIMPLES
AXIOMAS DE LOS NÚMEROS REALES
DE ORDEN
ADITIVO:
ANTISIMÉTRICO
TRICOTOMÍA
DE LA ADICIÓN Y MULTIPLICACIÓN
DISTRIBUTIVO - RECOLECTIVO
INVERTIVO
CONMUTATIVO
MODULATIVO
ASOCIATIVO
CLAUSURATIVO – UNÍVOCO
DE LA IGUALDAD
CANCELATIVO
MULTIPLICATIVO
ADITIVO
TRANSITIVO
SIMÉTRICO
REFLEXIVO
DICOTOMÍA