av Marco Doicela 3 år siden
251
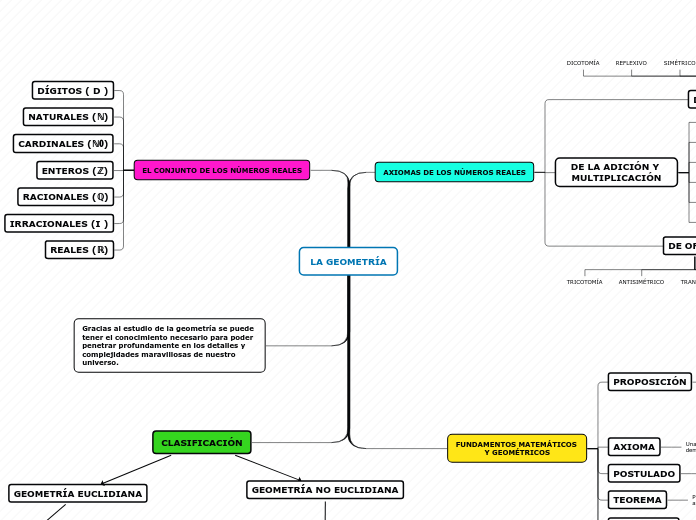
LA GEOMETRÍA
La geometría es fundamental para comprender las complejidades del universo. Se basa en varios conceptos matemáticos como axiomas, teoremas y proposiciones. Un axioma es una proposición evidente que no requiere demostración, mientras que un teorema necesita ser demostrado.