によって Yulieth Yamile Abaunza Malagon 2年前.
157
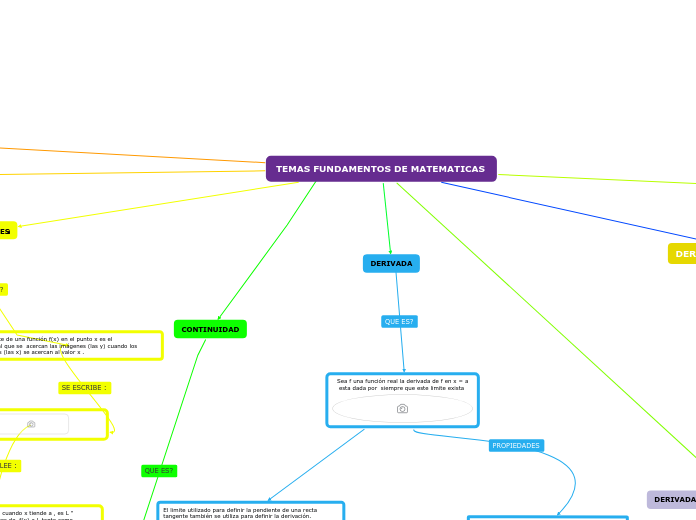
TEMAS FUNDAMENTOS DE MATEMATICAS
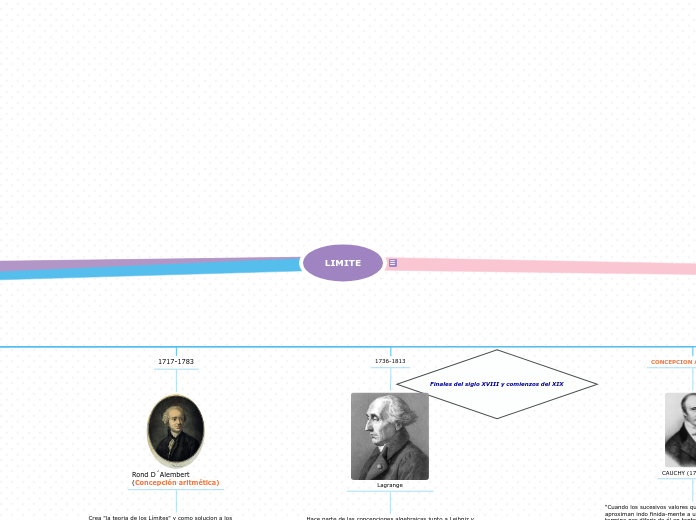
En matemáticas, las derivadas de orden superior se obtienen derivando repetidamente una función. La continuidad de una función en un punto se garantiza si la función está definida en dicho punto, el límite existe y coincide con el valor de la función en ese punto.