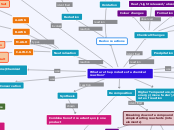
Equations of lines and planes
Sketching Planes
Using a line and multiple points we can come up with the equation of a plane
Vector and parametric equations of a plane
These equations can allow us to obtain any point on the plane
Can be determined in 4 ways
Cartesian equations of planes
need a point and a vector to derive the equation
Written in the form: Ax + By + Cz + D = 0
Cartesian equations of lines
Written in the form: Ax + By + C = 0
Symmetric Equations of lines in R3
Derived from parametric equations
Vector and parametric equations of lines
To find equations of lines we must be given two distinct points/one point along with a direction vector
Applications of Vectors
z
Finding torque
dot product is used when installing solar panels
Calculating work done
Scalar and Vector projects
A real life application includes computer animation.
Direction Angles
Projection of one vector onto another. You can think of it kind of like a shadow
Cross Product
Multiple methods are available for you to find the cross product. Find which one works best for you!
Finds the orthogonal of the vectors
Dot Product
Tells us the amount of force applied in the direction of motion
Vectors should be placed tail to tail
Angle x must be from 0 to 180 degrees
Forces and Vectors
Equilibrant of multiple forces
resultant and composition of forces yields combined force
Vectors can be expressed as forces and velocity
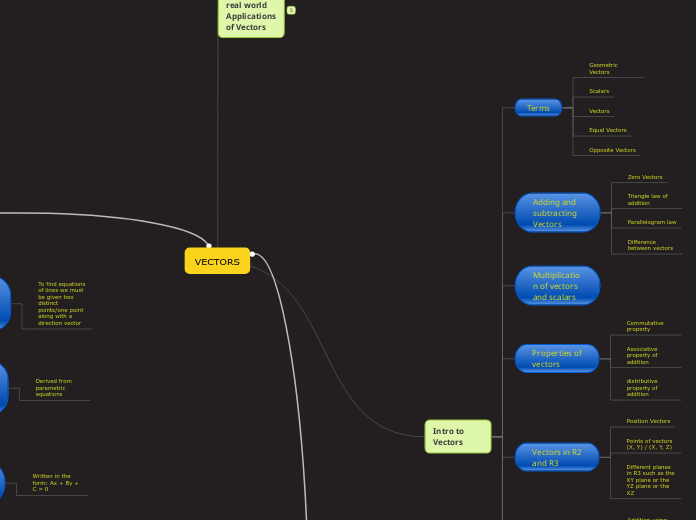
VECTORS
Learn more about how a small village on the banks of the Tiber River became the core of one of the most powerful ancient civilizations.
Intro to Vectors
Linear combinations of vectors
vectors in the form a(scalar)i(vector + b(scalar)j(vector) + c(scalar)k(vector) in R2
vectors in the form a(scalar)i(vector + b(scalar)j(vector) in R2
Operations of vectors in R3
Finding position vectors in R3
Addition of vectors using a method such as the parallelogram law
Using Pythagorean theorem to define two points
Operations of vectors in R2
Scalar multiplication using components
Addition using component form
Vectors in R2 and R3
Different planes in R3 such as the XY plane or the YZ plane or the XZ
Points of vectors (X, Y) / (X, Y, Z)
Position Vectors
Properties of vectors
distributive property of addition
Associative property of addition
Commutative property
Multiplication of vectors and scalars
Adding and subtracting Vectors
Difference between vectors
Parallelogram law
Triangle law of addition
Zero Vectors
Terms
Opposite Vectors
Equal Vectors
Vectors
Scalars
Geometric Vectors
Additional real world Applications of Vectors
sources: 1. https://testbook.com/learn/maths-application-of-vector/ 2. https://www.slideshare.net/Iftekharbhuiyan1/real-life-application-of-vector
Roller coasters
Navigating in air and water often uses vectors
The swinging of a pendulum
Sharpening pencil with a blade