by Igal Brener 5 years ago
468
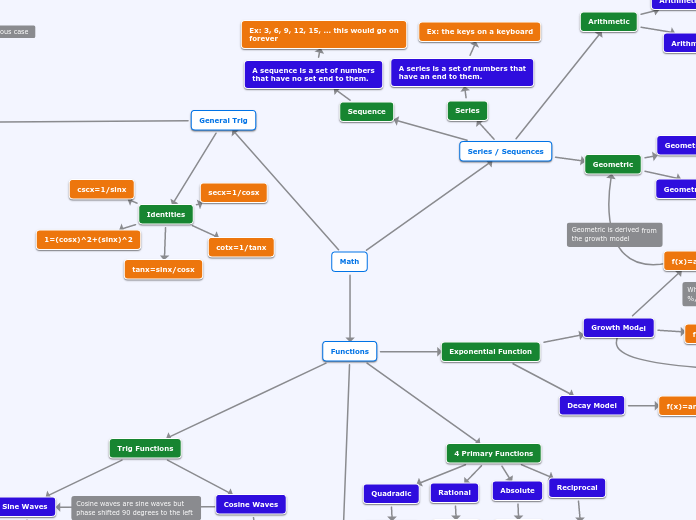
Math
The document provides an overview of various mathematical and financial concepts. It begins with financial applications, detailing the formulas for calculating both compounding and simple interest.
by Igal Brener 5 years ago
468

More like this
Sn=a(r^n-1)/r-1
ar^n-1
a+d(n-1)
Sn=n(2a+d(n-1))/2
Sn=n(a+tn)/2
Ex: 3, 6, 9, 12, 15, ... this would go on forever
Ex: the keys on a keyboard
This is the CAST rule
Angles for 45°
Angles for: 30° and 60°
h=asinB
A function where numbers can be any value within a set.
Ex: time it took to complete some task at any point you could say 1/2 of a second, 1 microsecond, 1 minute but there is a defined set if the task for example took 10 minutes.
tn=t(n-1)....
A function that calls upon previous numbers within the function.
Ex: the Fibonacci sequence that uses the previous numbers in the sequence to make the new number.
A function that has specific data set. Aka: several points in data.
Ex: # of students in a class, only a set # as you cannot have 1/2 of a student.
f(x)=A₀(1+i)^x
f(x)=ar^x
f(x)=ar^x (where r is a decimal / fraction)
f(x)=1/x
f(x)=|x|
f(x)=√x
f(x)=x^2
f(x)=acos(k(x-h))+c
f(x)=asin(k(x-h))+c
(x,y)---}((x/k)+h,ay+c)