Math Quadratics

More like this

Sample Mind Map

by juan ignacio soto

DEMONSTRATE MASTERY OF KNOWLEDGE AND UNDERSTANDING OF CULTURAL DIVERSITY ISSUES

by mohamad fathullah

System of Equation

by brittney adams

Factoring Mind Map

by Eric Schmidt

A (y) COORDINATE

Optimal Value

The Highest(Maximum or Lowest(Minimum) point on the parabola

Parabola meets Axis of Symmetry to split into two equivalent halves

A (x) coordinate

Axis of Symmetry

Direction of Opening

If a<0, the Parabola opens down

If a>0, the Parabola opens up.

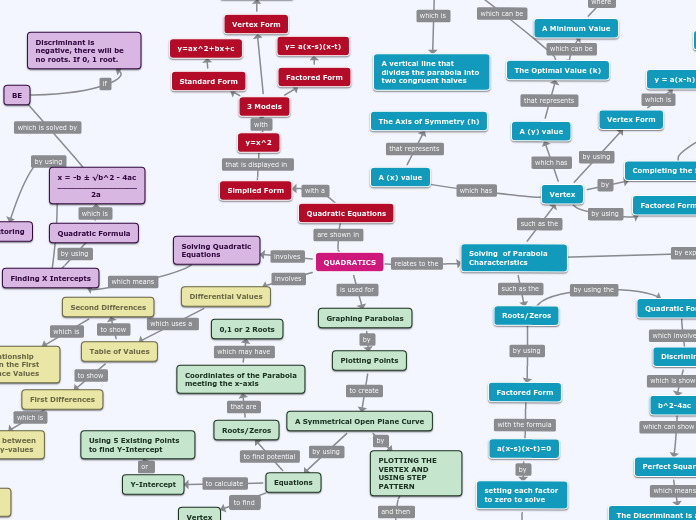
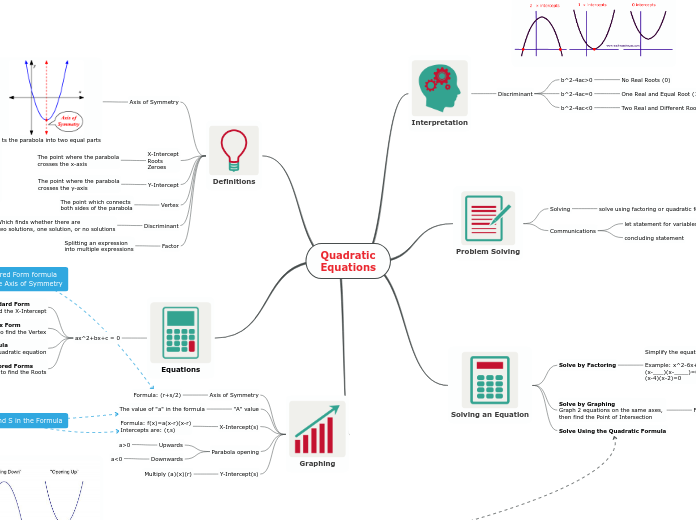
QUADRATICS

Differential Values

Table of Values

First Differences

The relationship between the consecutive y-values

A constant relationship states a linear relation

Second Differences

The relationship between the First Difference Values

A constant relationship states a quadratic relation

EXAMPLE

Graphing Parabolas

Plotting Points

A Symmetrical Open Plane Curve

PLOTTING THE VERTEX AND USING STEP PATTERN

Adding 5 more points onto the parabola from your equation

Equations

Y-Intercept

Using 5 Existing Points to find Y-Intercept

Coordiniates of the Parabola meeting the x-axis

0,1 or 2 Roots

Solving of Parabola Characteristics

The (a) value

Vertical Stretch/Compression

A magnitute change to the base parabola

a>1

A Vertical Stretch

0

A Vertical Compression

Vertex

The Roots (x1,x2)

The (h) value with x1+x2/2=h

Subsitituing h into the previous parbola equation to find the y/k of the vertex.

Converting Standard Form to Vertex Form

The (h,k) values

y = a(x-h)^2+k

(h,k) represent V(x,y)

y = 2(x-4)^2+7 V(4,7)

A (y) value

The Optimal Value (k)

A Minimum Value

The parabola opens up and is the lowest point on the parabola.

A Maximum Value

A vertical line that divides the parabola into two congruent halves

The parabola opens down and is the highest point on the parabola.

A (x) value

The Axis of Symmetry (h)

Roots/Zeros

a(x-s)(x-t)=0

setting each factor to zero to solve

2(x-4)(x+5)=0

x+5=0 x=-5

x-4=0 x=4

Discriminant

b^2-4ac

Perfect Square

The Discriminant is a perfect square, thus making it a rational number that does not need the Quadratic Formula.

Nature of Roots

b^2-4ac < 0

There are no Real Roots

Showing Imaginary Relations(i)

b^2-4ac = 0

There is 1 Real Root (Vertex is on x-intercept)

b^2-4ac > 0

There are 2 Real Roots

x=b2-4ac/2a

Solving Quadratic Equations

Finding X Intercepts

Completing the Square

Standard Form to Vertex Form

Isolating X for roots

Factoring

Standard Form to Factored Form

lal>1

Use Complex Trinominal Factoring

a=1

Use Simple Trinomial Factoring

Perfect Square Trinomial

Difference of Squares

a2 – b2 = (a + b)(a – b)

Quadratic Formula

x = -b ± √b^2 - 4ac ________________ 2a

BE

Discriminant is negative, there will be no roots. If 0, 1 root.

Quadratic Equations

Simplied Form

y=x^2

3 Models

Vertex Form

y=a(x-h)^2+k

Standard Form

y=ax^2+bx+c

Factored Form

y= a(x-s)(x-t)