A (y) COORDINATE
Optimal Value
The Highest(Maximum or Lowest(Minimum) point on the parabola
Parabola meets Axis of Symmetry to split into two equivalent halves
A (x) coordinate
Axis of Symmetry
Direction of Opening
If a<0, the Parabola opens down
If a>0, the Parabola opens up.
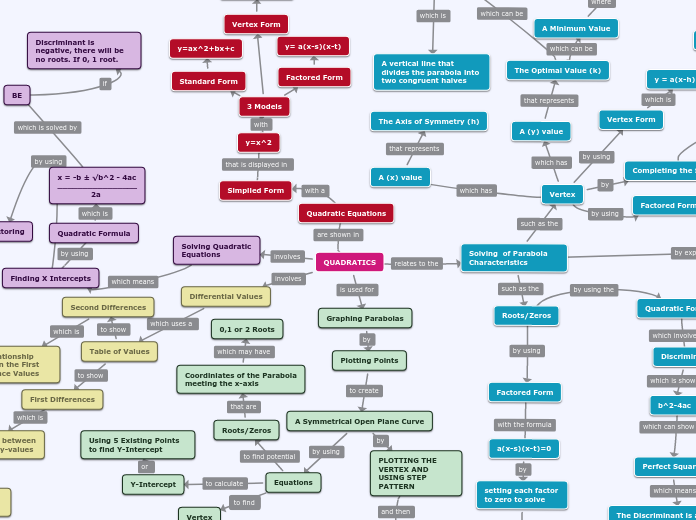
QUADRATICS
Differential Values
Table of Values
First Differences
The relationship between the consecutive y-values
A constant relationship states a linear relation
Second Differences
The relationship between the First Difference Values
A constant relationship states a quadratic relation
EXAMPLE
Graphing Parabolas
Plotting Points
A Symmetrical Open Plane Curve
PLOTTING THE VERTEX AND USING STEP PATTERN
Adding 5 more points onto the parabola from your equation
Equations
Y-Intercept
Using 5 Existing Points to find Y-Intercept
Coordiniates of the Parabola meeting the x-axis
0,1 or 2 Roots
Solving of Parabola Characteristics
The (a) value
Vertical Stretch/Compression
A magnitute change to the base parabola
a>1
A Vertical Stretch
0
A Vertical Compression
Vertex
The Roots (x1,x2)
The (h) value with x1+x2/2=h
Subsitituing h into the previous parbola equation to find the y/k of the vertex.
Converting Standard Form to Vertex Form
The (h,k) values
y = a(x-h)^2+k
(h,k) represent V(x,y)
y = 2(x-4)^2+7 V(4,7)
A (y) value
The Optimal Value (k)
A Minimum Value
The parabola opens up and is the lowest point on the parabola.
A Maximum Value
A vertical line that divides the parabola into two congruent halves
The parabola opens down and is the highest point on the parabola.
A (x) value
The Axis of Symmetry (h)
Roots/Zeros
a(x-s)(x-t)=0
setting each factor to zero to solve
2(x-4)(x+5)=0
x+5=0 x=-5
x-4=0 x=4
Discriminant
b^2-4ac
Perfect Square
The Discriminant is a perfect square, thus making it a rational number that does not need the Quadratic Formula.
Nature of Roots
b^2-4ac < 0
There are no Real Roots
Showing Imaginary Relations(i)
b^2-4ac = 0
There is 1 Real Root (Vertex is on x-intercept)
b^2-4ac > 0
There are 2 Real Roots
x=b2-4ac/2a
Solving Quadratic Equations
Finding X Intercepts
Completing the Square
Standard Form to Vertex Form
Isolating X for roots
Factoring
Standard Form to Factored Form
lal>1
Use Complex Trinominal Factoring
a=1
Use Simple Trinomial Factoring
Perfect Square Trinomial
Difference of Squares
a2 – b2 = (a + b)(a – b)
Quadratic Formula
x = -b ± √b^2 - 4ac
________________
2a
BE
Discriminant is negative, there will be no roots. If 0, 1 root.
Quadratic Equations
Simplied Form
y=x^2
3 Models
Vertex Form
y=a(x-h)^2+k
Standard Form
y=ax^2+bx+c
Factored Form
y= a(x-s)(x-t)