The goal of this map is to outline the major topics in congruence, constructions and similarity. It includes videos, worksheets and links to web resources. The audience is teachers.
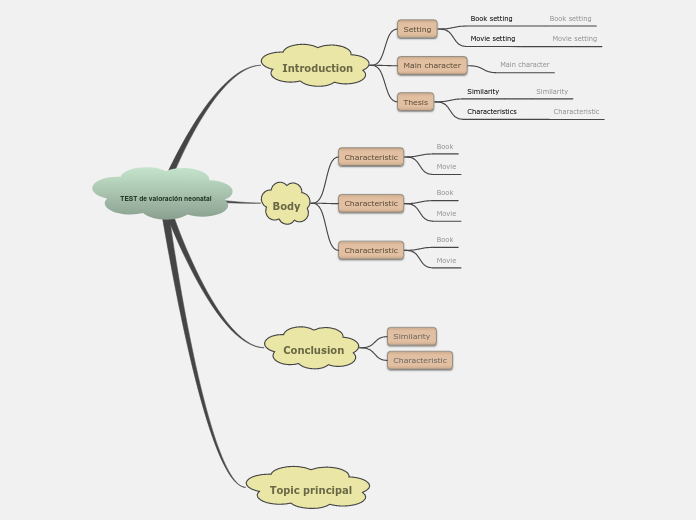
Congruence, Constructions and Similarity
Constructing Geometric Figures
Construction of Regular Polygons
The attached link is a great resource for showing how to construct regular polygons. It gives step by step instructions, including how to use a compass.
Inscribed Circle and Circumscribed Circle of Triangle
Theorem: The Inscribed Circle of a Triangle
The angle bisectors of a triangle ABC are concurrent at a point I (the incenter of the triangle) that is the center of a unique circle (the inscribed circle or incircle) that is tangent to the three sides AB, BC and AC.
Theorem: The Circumscribed Circle of a Triangle
The perpendicular bisectors of a triangle ABC are concurrent at point P (the circumcenter of the triangle) that is the center of a unique circle (the circumscribed circle) that passes through the three vertices A, B and C of the triangle.
The attached link shows the definition, a picture, how to construct each and a short assignment.
Compass and Straightedge Constructions
The attached link is a great resource for Geometric Constructions. Click on items in blue for details and directions on how to construct each. The two used most often are Line Segment Bisector and Angle Bisector. Learning how to construct perpendicular and parallel lines are also important.
Congruent Triangles
Definition: Two triangles are congruent if and only if there is correspondence of vertices of the triangles, such that the corresponding sides and corresponding angles are congruent.
Congruence is indicated by the symbol ≅.
For additional reading on congruent triangles, see the attached link.
Application of Congruent Triangles
View the link for a worksheet on congruent triangles.
Thales' Theorem
Theorem: Thales' Theorem
Any triangle ABC inscribed in a semicircle with diameter AB has a right angle at point C.
See the attached link for additional reading.
Isosceles Triangle Theorem
Theorem: Isosceles Triangle Theorem
The angles opposite the congruent sides of an isosceles triangle are congruent.
See the link for a proof of this theorem.
Triangle Inequality
Theorem: Triangle Inequality
The sum of the lengths of any two sides of a triangle is greater than the length of the third side.
The attached link creates a worksheet on Triangle Inequality.
Properties of Congruent Triangles
Similar Triangles
In order to be similar, two triangles must have the same shape but aren't necessarily the same size.
Definition: Similar Triangles and the Scale Factor
Triangle ABC is similar to triangle DEF if and only if corresponding angles are congruent and the ratios of lengths of corresponding sides are all equal. The common ratio of lengths of corresponding sides is called the scale factor from triangle ABC to triangle DEF.
For additional reading on similar triangles, see the attached link.
Application of Similar Triangles
View the link for a quiz and worksheet on similar triangles.
Properties of Similar Triangles