by Jared Hall 5 years ago
406
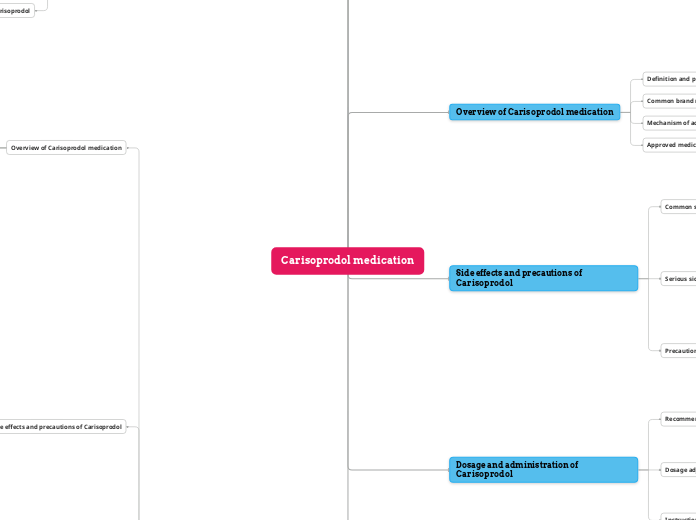
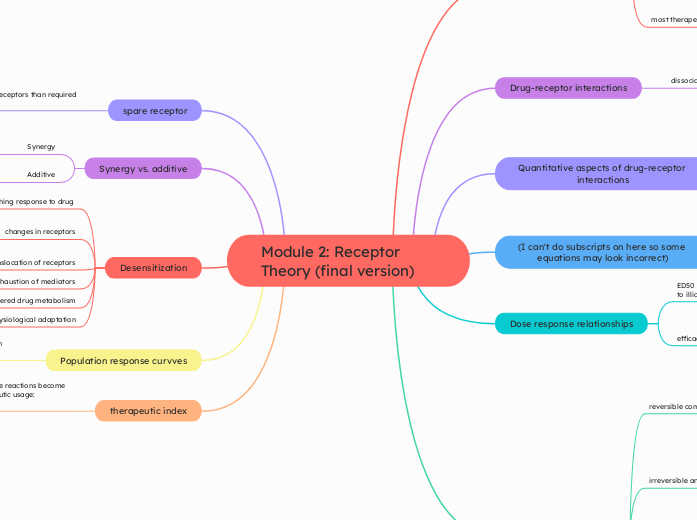
Module 2 Mind Map
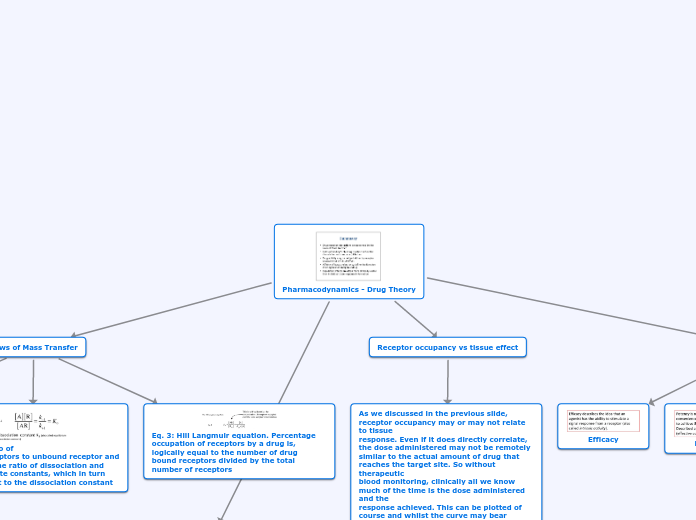
The relationship between drug concentration and its effects on the body is a fundamental concept in pharmacodynamics. Through various equations, such as the Hill-Langmuir equation, scientists can model the interaction between drugs and receptors.