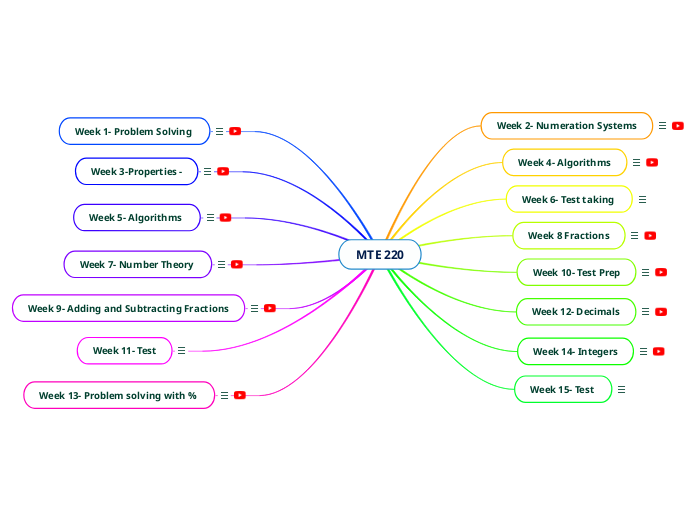
MTE 220

More like this

Pelletier MA9-1

by Len Pelletier

MTE 280 Investigational Quantity

by Betsy Aguilar

MTE 280 Numbers, Operations, & Proportional Reasoning, K-8 Teach

by Denisse Alejandra Diaz

Elementary Mathematics

by Elizabeth Flores

MTE 220

Week 13- Problem solving with %

Is- =

of- x (multiply)

what- n (unknown)

%- decimal

8%- 0.08

Use critical thinking when it comes to problem solving!

a) 8 is what % of 22? (should be around 1/3)

8 = n x 22

22 22

8 divided by 22 equal 0.36 with 36 repeating

Therefore it is 36%

A Students takes a test w/ 45 questions ad gets 37 correct. What % did they get on the test?

• divide 37 by 45
• equals .82 with the 2 repeating so the answer is 82%

7/8 as a decimal

• 7 divided by 8 equals 0.875

Practice problems

In the US, 13 out of 20 cans are recycled. what % of cans are recycled?

• you can either do 13/20 and find the equivalent which is 65/100. 65% is our answer
• 
  

https://www.youtube.com/watch?v=suAikQqJD34

Week 11- Test

Day 1

Took our test

Day 2

Reviewed tests answers

Week 9- Adding and Subtracting Fractions

Adding fractions with common denominator

examples using pictures will be in video

1/4 + 2/4= 3/4

when both of the fractions have the common denominator, you just need to add the number on the numerators

1/4+1/6=5/12

• because the number in the denominators are different, you have to find the least common nuliptle of the 2 numbers
• 4 and 6 have a LCM of 12

3/12+ 2/12=5/12

If there is a improper fraction, make sure to turn it into a mixed number

12/10-> 1 1/5

Multiplying Fractions

• multiplying fractions decreases the outcome

1/2 of 1/2= 1/4

multiply the numerators together and then multiply the denominators together

Division

2/3 divided by 4/5

do the inverse of the second fraction and then multiply them

2/3 x 5/4= 10/12

https://www.youtube.com/watch?v=ysKCXALX2sM

Week 7- Number Theory

Number Theories

• Types of numbers
• divisibility rules
• Factors

Fractions

• multiples

a is divisible by b if there is a number c that meets the requirement bxc=a

ex- 10 is divisible by 5 because 2x5=10

Divisibility Rules:

Endings

-by 2: 0,2,4,6,8

-by 5:0,5

-by 10:0

Sum of digits

-by 3: sum of digits is divisible by 3 ex 39- becuase 3+9=12 which is divisible by 3

-by 9: sum of digits is divisible by 9

Last digits

-by 4: last 2 digits are divisible by 4 ex 316

-by 8: last 3 digits are divisible by 8

6

-by 6: if it is divisible by BOTH 2 and 3

7

-by 7: double the last number and subtract the sum by the other numbers ex 826- 6 doubled is 12, then subtract 12 by 82

11

-by 11: "chop off"

Prime factorization

the figerprint or DNA if every composite number:

ALWAYS THE SAME

24 24

6 4 8 3

2 3 2 2 4 2

2 2

GCF; Greatest Common Factor

1. List Method

24: 1,2,3,8,12,24,4,6

36:1,2,3,4,6,9,12,18,36

GCF(24,36) : 12

1. Prime Factorization Method

24: 2x2x2x3

36: 2x2x3x3

2z2x3 = 12

Least Common Multiple

24:24,48,72,96

36: 36,72

The least common multiple is 72

https://www.youtube.com/watch?v=Df9h5t64NlQ

Week 5- Algorithms

Addition and Subtraction Algorithms

6 Addition algoritms

1.American Standard

256

+415

671

2.Partial Sum- adding from right to leaft and carr

346

+124

10

6

+ 4

470

3.Partial Sum w/ Place Value

346

+124

10

60

+400

470

4.Left to Right- work from the hundreds value to the ones

178

+269

300

130

+17

447

5.Expanded Notation

576 500+70+6

+ 279 +200+70+9

855 855

6.Lattice

5 7 6

+2 7 9

0 1 1

7 4 5

8 5 5

6 Subtraction algorithms

1.American Standard

645

-279

366

2.European/Mexican- instead of taking away from the top place values, you are adding to the bottom place values

3.Reverse Indian

4.Left to Right- solve going from left to right in all place values

5.Expanded Notation-same concept as addition just using multiplication

6.Integer Subtraction- following from right to left and allowing their to be negative numbers. Then solve

https://www.youtube.com/watch?v=TClOCPBYw10

Week 3-Properties -

Properties of addition, subtraction, and multiplication

Addition- to put together/join

Identity Property- a+0=a

ex- 4+0=4 , 3/5+0= 3/5

Commutative (order) Property- the order of the number doesn't matter when adding a+b=b+a

ex- 9+8=8+9

Associative (grouping) Property- grouping in different ways (a+b)+c= a+(b+c)

ex- (3+4)+8 = 3+(4+8)

Subtraction-

1. Take away
2. ex- 5-3
3. Comparison: its not adding or subracting
4. ex- how many more coins are in group A than in group B
5. Missing addend
6. ex- 3+ = 7

Multiplication- repeated addition

3x2 = 3 groups of 2 (2+2+2)

Identity Property of Multiplication- ax1 =a

ex- -3x1= -3

Zero Property of Multiplication- ax0=0

ex- 3x0=0 , 236x0=0

Commutative Property of Multiplication- axb=bxa

ex 3x7=7x3

Associative Property of Multiplication- (axb)xc = ax(bxc)

ex- (2x4)x4 = 2x(4x4)

Distributive Property of Multiplication- multiplying a number by a sum is the same as multiplying each number of the sum then adding them together

ex- 3x(6+1)

(3x6)+ (3x1)

18+3

21

https://www.youtube.com/watch?v=s9h-n95AXrc

Week 1- Problem Solving

Problem Solving

Gorge Playa Theory

1. Understand the Problem
2. what is it asking?
3. do I know what I am looking for?
4. Plan how to solve
5. trial and error
6. act out
7. work backwards
8. make organized list
9. make table
10. Implement the plan
11. -easier way?
12. be patient and persistant
13. try different plans
14. try different plan
15. look back- Reflect
16. does this make sense?
17. what did you learn?
18. was there and easier way to solve?

There are 12 basketball teams in a league. If each of the teams plays each of the other teams once and only play once, how many games take place?

team games

1 0

2 1

3 3

4 6

5 10

6 15

7 21

8 28

9 36

10 45

11 55

12 66

1 cant play itself which is why it has 0 games. On the second row, 1 and 2 play each other for one game. Third row, 1 and 2 played, 1 and 3 played but also 2 and 3 played which is why there are 3 games played. Fourth row we are adding 3 more games because 1 also played 4, 2 played 4 and 3 played 4. this continues with all 12 teams.

We can also see a pattern of adding up another number as each row goes down.

0+1=1

1+2=3

3+3=6

6+4=10

10+5=15

15+6=21

continued

ex- I have four 3-cent stamps and three 7-cent stamps. Using one or more of these stamps, how many different amounts of postage can I make?

Stamps alone (single) 7

stamps together 12 = 19 total

3,3,3,3

7,7,7

37,377,3777

337,3377,33777

3337,333777,3337777

33337,333377,3333777 = 19 total outcomes

https://www.youtube.com/watch?v=zhL3EMFSm6o

Week 15- Test

Test and mindmap

YAAAYUYYYYYY

Week 14- Integers

Positive and Negative Numbers- "the chip method"

• addition
• bring more chips into the circle
• when you are adding a negative number, that creates a zero pair which cancels out
• subtraction
• take ''chips" out of the groups
• which you are subtracting a positive by a negative, you take out the negative out of one of the zero pair +5- (-1) = 6
• multiplying
• +3 x +2 = 6
• 3 groups of 2
• -3 x +2 = -6
• commutative property applies
• when multiplying 2 negatives, "the opposite of" cover the negative of the first integer then use the opposite
• division
• video
• https://www.youtube.com/watch?v=_B1fuzmonO4
• 
  

Week 12- Decimals

Decimals

1- Thousands

9- Hundreds

4- Tens

3- Ones

.- decimal

5- Tenths

1- Hundredths

3- Thousandths

Smallest-> Greatest

0.3, 0378, 0.98, 0.23

0.23< 0.3< 0.378< 0.98

Adding and Subtracting Decimals

• The decimals have to be lined up on the correct place values

376.25

22.3 This is WRONG

376.25

22.30 This is CORRECT

Multiply

• These numbers do not need to line up

Division

https://www.youtube.com/watch?v=Val4TmjHXRY

Week 10- Test Prep

Test 2 Study Guide

• divisibility rules
• prime numbers- prime factorization tree
• true-false statements
• find GCF and LCM
• fractions- problem solving

Jim, Ken, Len and Max have a bag of bag of mini candy bars from trick or treating together. Jim took 1/4 of all bars, Ken and Len took 1/3 of all the bars. Max got the remaining 4 bars. How many bars were on the bag originally? How many bars did each get?

111 1111 1111 1

3/12 for Jim-12

4/12 for Ken-16

4/12 for Len- 16

1/12 for max- 4 bars

the numbers are over 12 because the LCM of 4 and 3 are 12

https://www.youtube.com/watch?v=kMPhdAXlM8k

Week 8 Fractions

Fractions

1. part-whole

boys/whole class

2.3/4- quotient

3.Ratio

boys/girls

Models

1. Surface Area

• 3 out of 4 pieces of pizza are gone

2.Length

3.Set (groups of things)

1 Whole = 4/4, 6/6

-fractional parts are equivalent parts

-the more my whole is divided by. the smaller my pieces get

https://www.youtube.com/watch?v=HBN568uvxi4

Week 6- Test taking

Day 1

The class took the 20 question test for the full class period

Day 2

With our tests being grades- we review frequent questions that were missed by the class

Week 4- Algorithms

Division and Multiplication Algorithms

Division- repeated subtraction

6➗2 division sign

6/2 division or fraction bar

division bar as well

Place Value Explicit

• filling in all of the place values when solving using long division

ex- John has 15 cookies. He puts 3 cookies in each bag. How many bags can he fill

Alternative Algorithm-repeated subtraction

197 cookies and 16 in each box. How many boxes are needed?

197-160- 10 boxes

37cookies left

37-32 2 boxes

5 cookies left

12 boxes in total

Standard Algoritm

Multiplication

Standard Algorithm- multiplying using partial products then adding together

Place Value

23

x14

4x3=12

4x20=80

10x3=30

+10x20=200

322

Expanded Notation

23 20+3

x14 x10+4.

300+ 20+2

322

Lattice- Video explaining



https://www.youtube.com/watch?v=W7cTvEcyyj4

Week 2- Numeration Systems

Numeration Systems

• created to record quantity
• base-10 system
• value changes in position

ex- 348

3- hundreds place

4- tens place

8- ones place

These are place values in base 10

348.27

2- one tenths

7 one hundredths

Base 10

0,1,2,3,4,5,6,7,8,9,10,11,12...

ones

tens

hundreds

Expanded Notation

ex- 348

3 hundreds+ 4 tens+ 8 ones

300+40+8 =348

(3x100)+(4x10)+(8x1)= 348

(3x10² )+ (4x10¹)+(8x10⁰) =348

Base 5

0,1,2,3,4,10₅ ,11₅, 12₅, 13₅, 14₅, 20_5,...

ones-5⁰

Fives- 5¹

twenty fives-5²

125s- 5³

how do you find 211₅ in base 10?

(2x5²)+(1x5¹)+(1x5⁰)

(2x25)+(1x5)+(1x1)

50+25+1

56

Base 3

0,1,2,10₃, 11₃,12₃, 20_3, 21₃

how do you find 33 in base 3?

27= 1

9= 0

3= 2

1= 0

https://www.youtube.com/watch?v=HJH0gBYhFiA