Numeration Systems
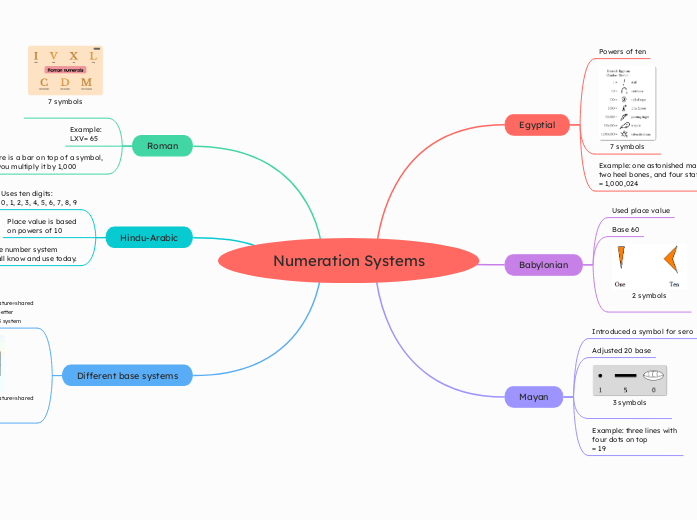
Different base systems
https://youtu.be/WFbh0YCtNCw?feature=shared
Base 2
uses numbers 1 & 0
Base 5
uses numbers 0-4
https://youtu.be/jyCsjd3N0jY?feature=shared
This video will show you how to better
understand how to use the base 5 system
Hindu-Arabic
This is the number system
that we all know and use today.
Place value is based
on powers of 10
Uses ten digits:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Partial Sums Algorithm
- A way to add in which sums are computed for each place value (ones, tens, hundreds, thousandths) separately. The partial sums are then added to get the final answer.
Lattice Algorithm for Addition
- Add single-digit numbers by place vale on top to the single-digit numbers on the bottom and record the results in a lattice. Then add the sums along the diagonals.
Scratch Algorithm for Addition
- Often referred to as a low-stress algorithm because it allows students to perform complicated additions by doing a series of additions that involve only two single digits.
Equal Additions Algorithm
- a method for subtraction where the same number is added to both the minuend (the number being subtracted from) and the subtrahend (the number being subtracted) in order to simplify the calculation
Counting-Up Algorithm
- counting up from a smaller number to a larger number to find the difference between the two numbers
Adding and Subtracting
Whole Numbers
Partial Products Algorithm
- break down each number into its place values and multiply each digit of one number by each digit of the other number separately, then add all the resulting "partial products" together to get the final answer
Standard Multiplication Algorithm
Lattice Algorithm for Multiplication
- Similar to the lattice Algorithm for addition, but instead using Multiplication.
Repeated Subtraction Strategy for Division
- repeatedly subtracting the divisor from the dividend until you reach zero, with the number of times you subtract being the answer to the division problem
Fair Sharing Strategy for Division
- dividing a quantity into equal parts, where each person or group receives the same portion of the whole
Standard Division Algorithm
Partial Quotient Algorithm
- breaking the problem into smaller parts, then adding the parts back together to get the final answer
Area Model Method for Division
Multiplication and Division
of Whole Numbers
The opposite of a number is better known as the additive inverse;
that is, the opposite of the number, a, is the number which must be added to a to produce the additive identity 0: a+?=0
This quantity is often referred to as the opposite of, a, and is written -a
Chip Model to find the Opposite Integer and Absolute Value
- Represent positive integers with one color chip (like blue) and negative integers with another color chip (like red), where a pair of chips with opposite colors would always cancel each other out to zero
Number Line to find the Opposite Integer and Absolute Value
- An opposite integer is on the other side of 0 but the same distance from zero.
Integers
- A whole number (not a fractional number) that can be positive, negative, or zero
Ordering Integers
Multiplying and Dividing Integers: Pattern Approach
Chip Model and Number Line Model for Division with Integers
Chip Model and Number Line Model for Multiplication with Integers
Chip Model and Number Line Model for Subtraction with Integers
Chip Model and Number Line Model for Addition with Integers
Operations with Integers
Dividing Fractions
Multiplying Fractions
Subtracting Fractions using Area Model
Adding Fractions using Area Model
Ordering Fractions
Interpretations of Fractions
- Fractions as parts of wholes (or parts of sets)
- Fractions as division of two numbers
- Fractions as ratio of two quantities
-Fractions as operators
- Fractions as measures
Formal Definition
- The set of numbers that can be written in the form a/b, where b≠0 and a and b are both integers is called the Rational Numbers
Fractions
Dividing Decimals using Grid Model
Multiplying Decimals Using Grid Model
Multiplying and Dividing Decimals using Grid Model
Adding and Subtracting Decimals using Grid Method
Subtopic
Decimals and Percents
Percents
Definitions:
- Divisibility: If a number is completely divisible by another number then the quotient will be a whole number and the remainder will be zero.
- Factor: A number or algebraic expression that divides another number or expression evenly
- Multiple: The numbers you get when you multiply a certain number by an integer. For example, multiples of 5 are: 10, 15, 20, 25, 30…etc.
- Divisible: A number goes evenly (with no remainder) into a number. For example, 2 goes evenly into 34 so 34 is divisible by 2.
- Divides: One integer can be divided evenly into another integer, leaving no remainder
- Divisor: The number by which the dividend is divided to obtain the quotient
Factors Using Cuisenaire Rods
- The length of each of the rods is a multiple of the length of the shortest rod
Prime Factorization to find GCF
- First break down each number into its prime factors, then identify the common prime factors between all the numbers and multiply them together; the product of those common prime factors is the GCF
Venn Diagram to find GCF
Using Cuisenaire Rods to find GCF
Greatest Common Factor
- The largest positive integer by which both integers can be divided
Prime Factorization to find LCM
- This method is similar to the Venn Diagram Method
1. Find the prime factorization of the given numbers
2. Take each of the primes that are factors of either of the given numbers
3. The LCM is the product of these primes, each raised to the greatest power of the prime that occurs in either of the prime factorizations
Venn Diagram to find LCM
The Intersection of Sets Method to find LCM
- creating sets of multiples for each given number, then finding the smallest element that exists in the intersection of all those sets
Using Cuisenaire Rods to find LCM
- Build "trains" with the rods, where the length of the train represents a multiple of the number each rod represents, and the LCM is the length of the shortest train where both sets of rods line up perfectly, meaning they have the same length at that point
Least Common Multiple
- The smallest number that two or more numbers can divide into evenly
Divisibility
Definition: Finding which prime numbers multiply together to make the original number.
Example:
To do so, first dividing the number into a common/well-known factor pair and then proceeding to further divide each factor until prime factors are determined.
Key Idea: Dividing the number by a prime factor repeatedly until it is exhausted.
Factor Trees: A useful, visual tool for finding the prime factorization of a number.
The Division-by-Prime Method
- Divide the given number by the smallest prime number
Prime Factorization
Prime Numbers: Natural numbers that are divisible by only 1 and the number itself
Composite Numbers: any positive integers or natural numbers that have more than two factors
Integers
-
List Method for finding Factors
- Find all of the factor pairs
Array Method for finding Factors
- A visual technique used in math education to find the factors of a number by drawing rectangular arrays where the dimensions of the array represent the factor pairs of that number
Prime and Composite Numbers
Roman
If there is a bar on top of a symbol,
then you multiply it by 1,000
Example:
LXV= 65
7 symbols
Mayan
Example: three lines with
four dots on top
= 19
3 symbols
Adjusted 20 base
Introduced a symbol for sero
Babylonian
2 symbols
Base 60
Used place value
Egyptial
Example: one astonished man,
two heel bones, and four staffs
= 1,000,024
7 symbols
Powers of ten