by Amanda Simba 4 years ago
633
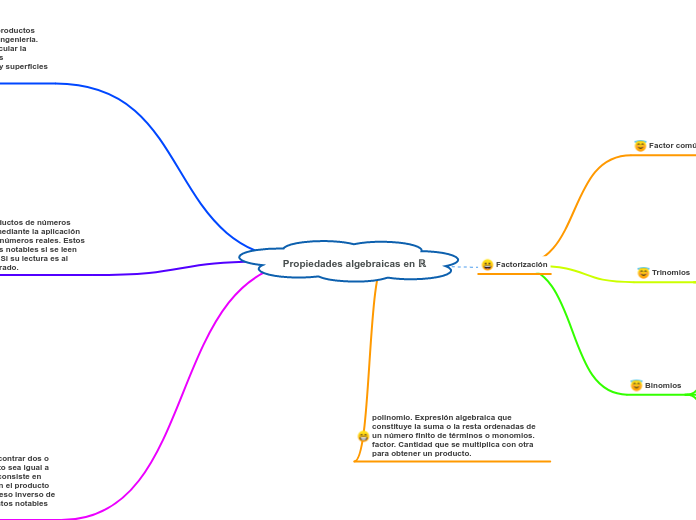
Propiedades algebraicas en ℝ
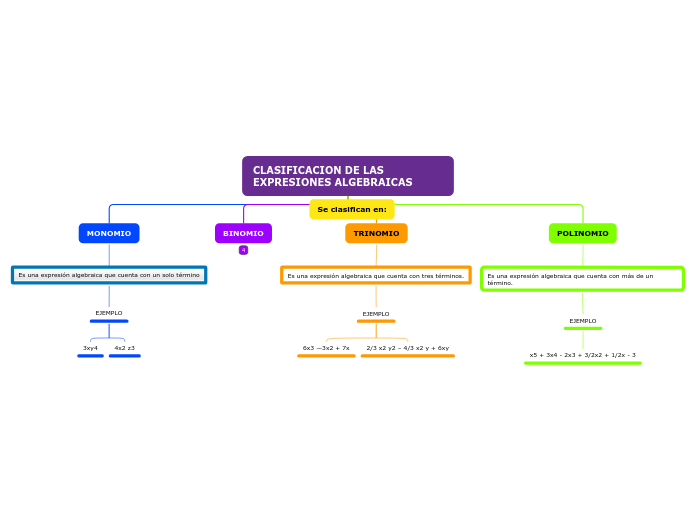
El proceso de descomponer una expresión algebraica en productos de dos o más factores se conoce como factorización. Este método es fundamental en matemáticas e ingeniería, ya que permite simplificar y resolver ecuaciones complejas.