by AMANDA CAROLINA QUEZADA SANMARTIN 4 years ago
367
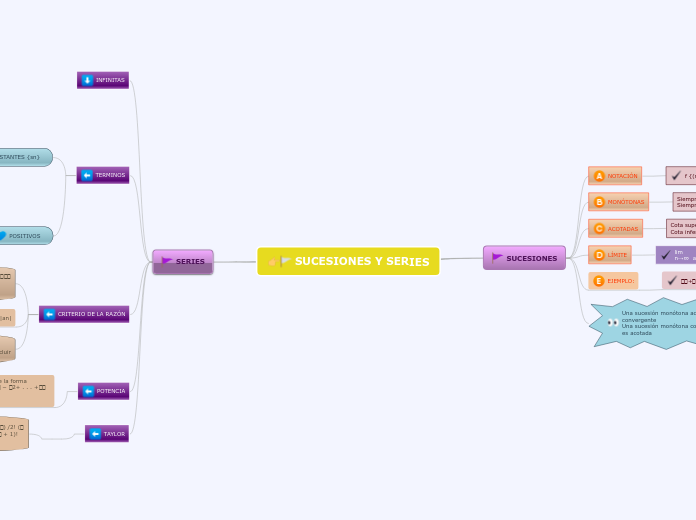
SUCESIONES Y SERIES
Las sucesiones y series son conceptos fundamentales en el análisis matemático. Las sucesiones son listas ordenadas de números que pueden ser acotadas o monótonas, es decir, que siempre crecen o decrecen.