by Rosa Ramírez 2 years ago
145
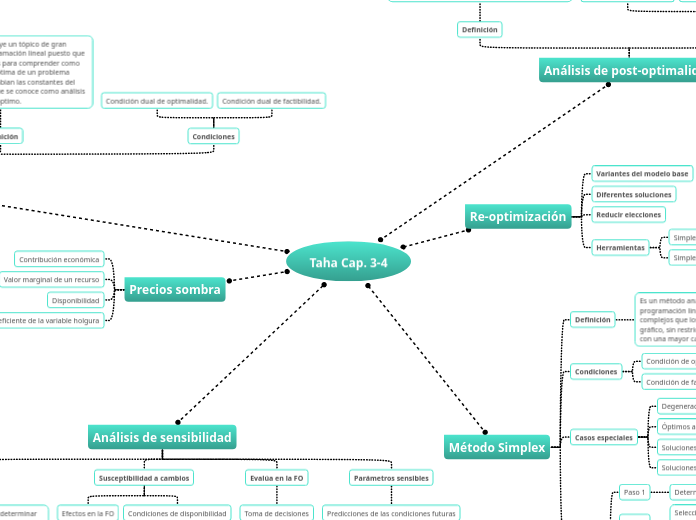
Taha Cap. 3-4
La dualidad es un concepto fundamental en la programación lineal, proporcionando las bases teóricas para entender cómo varía la solución óptima de un problema al modificarse las constantes del modelo matemático.