door francina caro 5 jaren geleden
289
IOA4
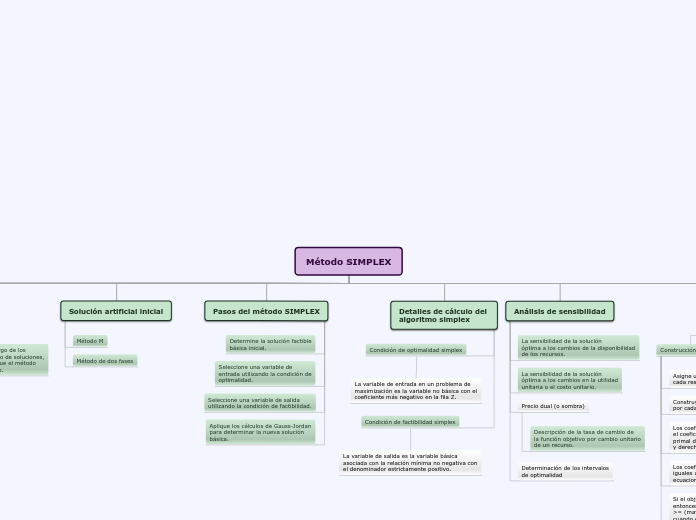
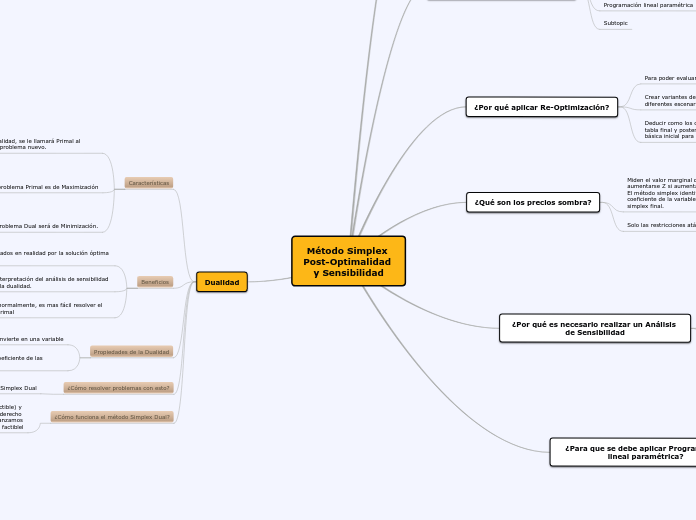
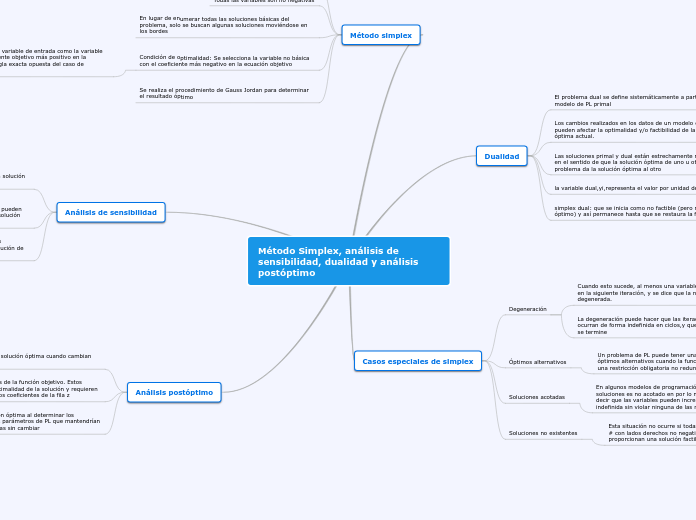
El método SIMPLEX es una técnica iterativa usada en la optimización de problemas lineales, moviéndose a lo largo de los bordes del espacio de soluciones sin cruzarlo. El análisis de sensibilidad evalúa cómo la solución óptima responde a cambios en los costos unitarios y la disponibilidad de recursos, determinando intervalos y precios duales.