av Matthew Jenkins 3 år siden
142
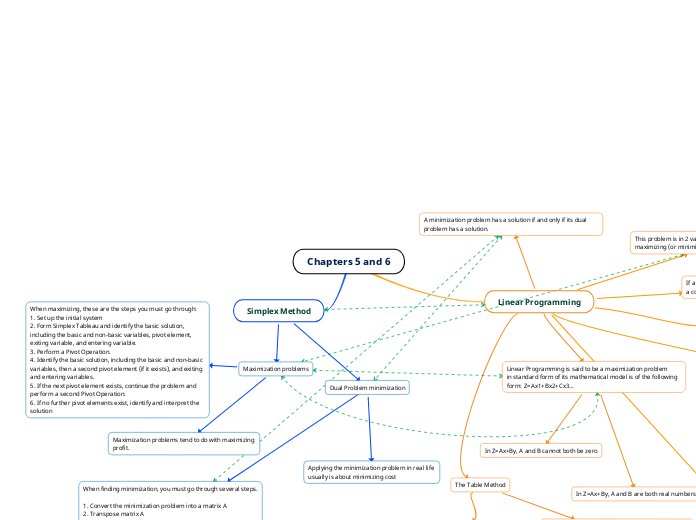
Chapters 5 and 6
The text provides a detailed guide on solving maximization and minimization problems using the Simplex Method, which is a key technique in linear programming. For maximization problems, the procedure involves setting up the initial system, forming the Simplex Tableau, identifying basic and non-basic variables, and performing pivot operations until no further pivot elements exist.