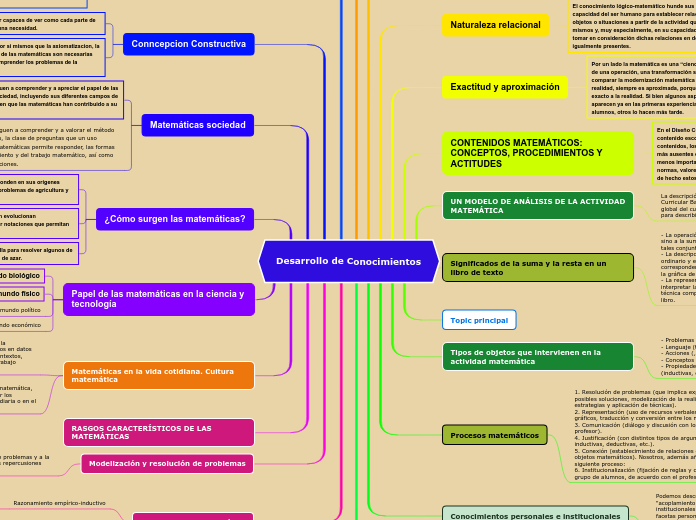
Desarrollo de Conocimientos
The part of speech is a category to which a word is assigned according to its syntactic functions. In English the main parts of speech are noun, pronoun, adjective, determiner, verb, adverb, preposition, conjunction, and interjection.
Razonamiento matemático
Formalización y abstracción
La formalización, precisión y ausencia de ambigüedad del conocimiento matemático debeser la fase final de un largo proceso de aproximación a la realidad, de construcción deinstrumentos intelectuales eficaces para conocerla, analizarla y transformarla
Razonamiento empírico-inductivo
El proceso histórico de construcción de las matemáticas nos muestra la importancia del razonamiento empírico-inductivo que, en muchos casos, desempeña un papel mucho más activo en la elaboración de nuevos conceptos que el razonamiento deductivo.
Modelización y resolución de problemas
El dar un papel primordial a la resolución de problemas y a la actividad de modelización tiene importantes repercusiones desde el punto de vista educativo.
RASGOS CARACTERÍSTICOS DE LAS MATEMÁTICAS
Matemáticas en la vida cotidiana. Cultura matemática
Capacidad para discutir o comunicar información matemática, cuando sea relevante, y competencia para resolver los problemas matemáticos que encuentre en la vida diaria o en el trabajo profesional.
Capacidad para interpretar y evaluar críticamente la información matemática y los argumentos apoyados en datos que las personas pueden encontrar en diversos contextos, incluyendo los medios de comunicación, o en su trabajo profesional.
Papel de las matemáticas en la ciencia y tecnología
A conjunction is a word like 'if' 'but' or 'and' which is used to connect sentences or clauses together.
El mundo económico
El mundo político
El mundo físico
Subordinating conjunctions are conjunctions that are used at the beginning of subordinate clauses. Some examples of these conjunctions are: although, after, before, because, how, if, once, since, so that, until, unless, when etc.
Nuestro mundo biológico
Coordinating conjunctions always connect phrases, words, and clauses. They are: for, and, nor, but, or, yet, so.
¿Cómo surgen las matemáticas?
A preposition is one of the most exciting parts of grammar. A preposition is used to describe the location of something in relation to something else.
La teoría de la probabilidad se desarrolla para resolver algunos de los problemas que plantean los juegos de azar.
When a preposition consists of more than one word, it is called double preposition.
into, within, upto etc.
Los diferentes sistemas de numeración evolucionan paralelamente a la necesidad de buscar notaciones que permitan agilizar los cálculos aritméticos.
Compound preposition consists of two or more words.
on behalf of, according to, in front of, from across, etc.
Muchos aspectos de la geometría responden en sus orígenes históricos, a la necesidad de resolver problemas de agricultura y de arquitectura.
When a preposition consists of one word it is called single or simple preposition.
in, at, on, to for, of, from, up, after, over, under, with, etc.
Matemáticas sociedad
An interjection is used to express emotion in a sentence.
Think of other interjections!
Que los alumnos lleguen a comprender y a valorar el método matemático, esto es, la clase de preguntas que un uso inteligente de las matemáticas permite responder, las formas básicas de razonamiento y del trabajo matemático, así como su potencia y limitaciones.
Que los alumnos lleguen a comprender y a apreciar el papel de las matemáticas en la sociedad, incluyendo sus diferentes campos de aplicación y el modo en que las matemáticas han contribuido a su desarrollo.
Conncepcion Constructiva
An adverb is used to describe a verb, but it can also describe an adjective or another adverb.
Adverbs normally help paint a fuller picture by describing how something happens.
Los estudiantes deben ver por si mismos que la axiomatizacion, la genealizacion la abstaccion de las matemáticas son necesarias con el fin de con el fin de comprender los problemas de la naturaleza y la sociedad
Just, Afterward, Soon, Currently
Los alumnos deberían de ser capaces de ver como cada parte de las matemáticas satisfacen una necesidad.
Carefully, Slowly
Concepción idealista-platonica
A numeral is a word or phrase that describes a numerical quantity.
Some theories of grammar use the word 'numeral' to refer to cardinal numbers that act as a determiner to specify the quantity of a noun, for example the 'two' in 'two hats'.
El alumno por si solo poda resolver las aplicaciones problemas que se le presenten.
One, two..
Adquirir estructuras fundamentales de las matemáticas de forma axiomática
First, second..
TRANSPOSICIÓN DIDÁCTICA
La expresión "transposición didáctica"6
hace referencia al cambio que el
conocimiento matemático sufre para ser adaptado como objeto de enseñanza. Como
consecuencia se producen diferencias en el significado de los objetos matemáticos entre
la "institución matemática" y las instituciones escolares. Por ejemplo, los usos y
propiedades de las nociones matemáticas tratadas en la enseñanza son necesariamente
restringidos. El problema didáctico se presenta cuando, en forma innecesaria, se muestra
un significado sesgado o incorrecto.
Conocimientos personales e institucionales
Podemos describir metafóricamente el aprendizaje como "acoplamiento progresivo" entre significados personales e institucionales en una clase. Es importante diferenciar las facetas personal e institucional de los conocimientos matemáticos para poder describir y explicar las interacciones entre el profesor y los alumnos en los procesos de enseñanza y aprendizaje.
Procesos matemáticos
1. Resolución de problemas (que implica exploración de posibles soluciones, modelización de la realidad, desarrollo de estrategias y aplicación de técnicas).
2. Representación (uso de recursos verbales, simbólicos y gráficos, traducción y conversión entre los mismos).
3. Comunicación (diálogo y discusión con los compañeros y el profesor).
4. Justificación (con distintos tipos de argumentaciones inductivas, deductivas, etc.).
5. Conexión (establecimiento de relaciones entre distintos objetos matemáticos). Nosotros, además añadimos el siguiente proceso:
6. Institucionalización (fijación de reglas y convenios en el grupo de alumnos, de acuerdo con el profesor)
Tipos de objetos que intervienen en la actividad matemática
- Problemas y situaciones (cuestiones, ejercicios, etc.)
- Lenguaje (términos, expresiones, gráficos, etc.)
- Acciones (, técnicas, algoritmos, etc.)
- Conceptos (definiciones o reglas de uso)
- Propiedades de los conceptos y acciones - Argumentaciones (inductivas, deductivas, etc.)
Topic principal
Significados de la suma y la resta en un libro de texto
- La operación de sumar no se refiere a la unión de conjuntos, sino a la suma de números que expresan los cardinales de tales conjuntos.
- La descripción de la operación de sumar se hace en lenguaje ordinario y en forma general. El niño debe ponerla en correspondencia con los símbolos numéricos del ejemplo y con la gráfica de la recta numérica.
- La representación mediante la recta numérica sugiere interpretar la suma como "seguir contando". Esta es una técnica completamente diferente, que no se ha descrito en el libro.
UN MODELO DE ANÁLISIS DE LA ACTIVIDAD MATEMÁTICA
La descripción de los contenidos matemáticos en el Diseño Curricular Base puede ser adecuada para una planificación global del currículo, pero consideramos que es insuficiente para describir la actividad de estudio de las matemáticas.
CONTENIDOS MATEMÁTICOS: CONCEPTOS, PROCEDIMIENTOS Y ACTITUDES
An article is a word used to modify a noun, which is a person, place, object, or idea. Technically, an article is an adjective, which is any word that modifies a noun.
En el Diseño Curricular Base (MEC, 1989) se entiende por contenido escolar tanto los que habitualmente se han considerado contenidos, los de tipo conceptual, como otros que han estado más ausentes de los planes de estudio y que no por ello son menos importantes: contenidos relativos a procedimientos, y a normas, valores y actitudes. En la escuela los alumnos aprenden de hecho estos tres tipos de contenidos.
It refers directly to a specific noun or groups of nouns.
The breakfast on my plate.
A pronoun is a word that can be used in place of a noun, typically after the noun itself has already been stated.
Por un lado la matemática es una “ciencia exacta”, los resultados
de una operación, una transformación son unívocos. Por otro, al comparar la modernización matemática de un cierto hecho de la realidad, siempre es aproximada, porque el modelo nunca es exacto a la realidad. Si bien algunos aspectos de esta dualidad aparecen ya en las primeras experiencias matemáticas de los alumnos, otros lo hacen más tarde.
The personal pronouns are I, you, he, she, it, we, they. More often than not (but certainly not always), they replace nouns representing people.
Naturaleza relacional
An adjective is a word that's used to describe a specific noun and to provide more detail to the listener.
El conocimiento lógico-matemático hunde sus raíces en la capacidad del ser humano para establecer relaciones entre los objetos o situaciones a partir de la actividad que ejerce sobre los mismos y, muy especialmente, en su capacidad para abstraer y tomar en consideración dichas relaciones en detrimento de otras igualmente presentes.
Expresses a comparison between two entities or groups of entities in quality or degree.
Exactitud y aproximación
He is taller than she is.
Estructura interna
A noun is defined as a person, place, thing or idea. Proper nouns always begin with a capital letter. Common nouns, which are general words, such as 'cars,' are not capitalized.
La insistencia sobre la actividad constructiva no supone en ningún caso ignorar que, como cualquier otra disciplina científica, las matemáticas tienen una estructura interna que relaciona y organiza sus diferentes partes. Más aún, en el caso de las matemáticas esta estructura es especialmente rica y significativa.
Proper nouns are the names of specific people or places. They should always begin with a capital letter.
Mary, Paris
Lenguaje y comunicación
A verb is an action word or 'doing' word that signifies movement in some way.
Gracias a la amplia utilización de diferentes sistemas de notación simbólica (números, letras, tablas, gráficos, etc,), las matemáticas son útiles para representar de forma precisa informaciones de naturaleza muy diversa, poniendo de relieve algunos aspectos y relaciones no directamente observables y permitiendo anticipar y predecir hechos situaciones o resultados que todavía no se han producido.
A verb with its own meaning: a verb that is not an auxiliary verb.
Create sentences
They have it.