av CARLOS ALBERTO LASSO PINEDA 4 år siden
329
Mer som dette
Type in the name of the multiple-perspectives text.
Example: Bridge to Terabithia by Katherine Paterson
Identify an important issue from the text that is being presented from different angles. Type it in.
Example: Jesse's drawing talent.
Decide on the first point of view you are going to present.
Type in the name of the character (it can either be the main character or one of the supporting characters) whose point of view belongs to.
Example: Jesse Oliver Aarons, Jr., the main character of the novel, a fifth-grader living in a rural Southern area.
La formación docente debe basarse no solo en una sólida base metodológica que garantice una adecuada cobertura y calidad, sino también como base para una propuesta conceptual que permita a los docentes desplegar la educación que necesita la sociedad colombiana en el nuevo siglo. El área temática de un profesor de matemáticas se puede distinguir de lo que llamamos matemáticas escolares. En la actualidad, lo que entenderemos a través de la matemática escolar es una forma de entender el conocimiento matemático y el conocimiento difundido en el ámbito escolar, y estos conocimientos y conocimientos tienen el punto de vista del conocimiento científico.
Hacia una política de formación de maestros
El Ministerio de Educación debe formular una serie de lineamientos para la formación docente que aseguren que este sea uno de los espacios que puedan producir los cambios profundos que necesita la educación de nuestro país. Por tanto, la formación del profesorado debe entenderse como un proceso para que el sujeto se convierta en un profesional en un campo temático específico: la educación matemática.
El desarrollo de este proceso incluye las siguientes etapas:
Investigación
Innovación
Actualización
Profesionalización
Sobre la lectura
Factores que constituyen o determinan un currículo
Los criterios para la selección de metodologías y recursos didácticos
La organización espacio/temporal de los contenidos que bien puede ser para asignaturas, por modelos (modograficos) por proyectos pedagógicos, por campos conceptuales, etc.
Los criterios para secuenciar los contenidos
Los criterios para selección de contenidos
Los propósitos de formación, por nivel y siclo
La enunciación de los principios
Type in a relevant quote that highlights the character's point of view towards
Los lineamientos curriculares están diseñados para promover su aprendizaje y uso. ¿Surgen de la pregunta de qué enseña? ¿Qué aprendió? En la escuela se relaciona con el currículo, plan de estudios, evaluación y promoción de los estudiantes. Buscan la capacidad de la comunidad para considerar de forma independiente el proceso educativo de la escuela, la comunidad y el mundo..
Try following a citation format: author's name, chapter, and page.
Example: 'Jesse drew the way some people drank whiskey. (...) Lord, he loved to draw. (...) When he was in first grade, he told his father that he wanted to be an artist when he grew up.' (Paterson, 2. 7)
Posiciones sobre el origen y la naturaleza de las Matemáticas a través de la historia
What type of narration introduces the viewpoint?
Choose an answer:
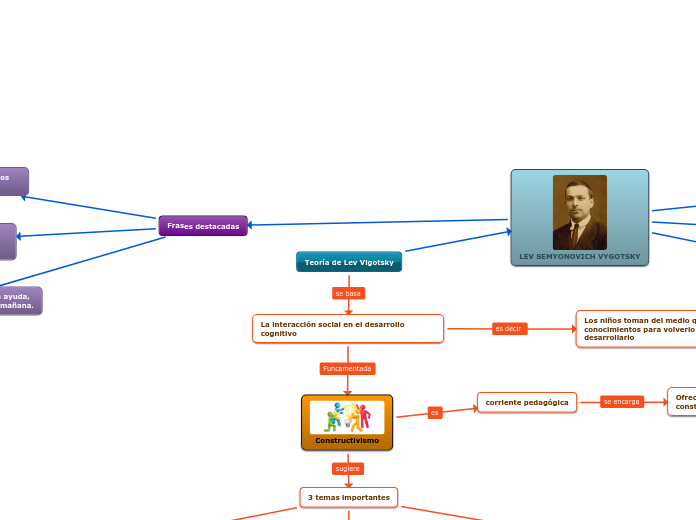
El Constructivismo
Está estrechamente relacionado con el intuicionismo porque también considera que las matemáticas son una creación de la mente humana, y que solo aquellos objetos matemáticos que pueden ser construidos mediante procedimientos finitos a partir de objetos primitivos tienen existencia real.
El Intuicionismo
Es la elaboración que hace la mente a partir de lo que percibe a través de los sentidos, es el estudio de aquellas construcciones mentales cuyo origen se identifica con la realización de números naturales. El principio básico es que las matemáticas se pueden construir; que tienen que partir de lo dado intuitivamente, y que sólo hay en ellos lo que se ha construido mentalmente con la ayuda de la intuición.
El Formalismo
Se reconoce que la matemática es la creación del pensamiento humano, comienza con las inscripciones de símbolos en el papel, todos los contenidos deben estar claramente definidos y no hay posibilidad de error.
El Logicismo
Se considera que la matemática es una rama de la lógica, con vida propia, pero con los mismos orígenes y métodos, la lógica es una ciencia que precede a otras ciencias, que contiene todas las ideas y principios en los que se basan todas las ciencias.
Existen dos clases de lógica; la deductiva y la inductiva.
El Platonismo
Esto trata a las matemáticas como un sistema de verdad, que ya existe y siempre es independiente del hombre. El platonismo reconoce que la relación entre figuras geométricas, operaciones y aritmética es un poco misteriosa para nosotros.
Contexto para la evaluaciòn
La nueva ley de educación ha realizado cambios importantes en el sistema educativo de Colombia, lo que exige que las evaluaciones sean cualitativas. Aquí parece necesario estipular que lo cualitativo no excluye lo cuantitativo. La evaluación cualitativa debe ser formativa, continua, sistemática y flexible, y su foco está en el propósito de generar y recolectar la información necesaria sobre el proceso de enseñanza dentro y fuera del aula.
Registros de evaluacion
Todas las instituciones son libres de desarrollar sus propios planes educativos, por lo que pueden elegir sus propias estrategias y métodos de enseñanza, lo que significa que es necesario aclarar el estado de eficiencia esperado en cada situación. El plan de estudios real debe ajustarse al plan de estudios formal descrito en el programa educativo y, en este caso, debe estar relacionado con el plan de aprendizaje de matemáticas que lo acompaña.
Lecturas de los indicadores de logros curriculares
Para diferentes observadores, los indicadores de logro propuestos por los estudiantes a partir de la situación problema pueden plantear diferentes hipótesis sobre el estado de ciertos procesos en el desarrollo de conocimientos básicos, a menos que estos observadores tengan la misma base teórica de análisis. La lectura dependerá principalmente del interés o foco específico de la observación.
Elementos para la evaluación de logros formativos y cognitivos
Un factor importante a recordar es la diferencia entre la respuesta del estudiante y la solución. El primero es una especie de acuerdo entre el sujeto y él mismo, y el segundo pertenece al conocimiento formal. Toda evaluación educativa es un juicio que compara propósito y deseo con la realidad que brinda el proceso, por lo que la evaluación debe ser más un reflejo que una herramienta de medición. Una parte importante de la enseñanza es asegurar que las respuestas de los estudiantes enfrenten soluciones, especialmente en situaciones en las que las respuestas no pueden aceptarse razonablemente como soluciones. La evaluación debe ser explicada en todos los sentidos y direcciones: la retroalimentación de los estudiantes es también la evaluación de los cursos, los profesores y las estrategias de trabajo o su desempeño.
Orientaciones para la evaluación
Los estudiantes deben ser evaluados continuamente con conductas que representen su trabajo diario: su actitud, persistencia, interés, participación, capacidad para distinguirse en un campo o disciplina específico, capacidad para absorber y comprender información y procedimientos, y mejorar gradualmente para comprender, analizar, Métodos de creación y resolución de problemas, y su creatividad o tendencia a buscar nuevos métodos o respuestas a situaciones. Los elementos incluidos aquello son los siguientes:
La capacidad de reflexionar, criticar, sobre lo que se aprende, lee o escribe.
La capacidad de lectura y escritura de temas relacionados con la tarea.
El interés por ampliar los conocimientos discutidos en el aula.
La participación individual en tareas colectivas.
La adquisición de destrezas.
Los estilos de trabajo: solitario y colectivo.
Las estrategias y procedimientos utilizados para plantear y resolver problemas.
La capacidad para interpretar, plantear y resolver problemas.
La capacidad para aplicar los conocimientos.
Las formas de comunicación de concepciones y conceptos.
El estado de conceptualización alcanzado frente a los saberes formales.
La comprensión de los conocimientos básicos en un momento dado.
Los cambios que se presentan en las concepciones mediante la participacion activa de los estudiantes durante la construccion de los conocimientos.
Las concepciones de los alumnos sobre los conceptos.
Estructura curricular
A partir de esta visión global y comprehensiva de las operaciones matemáticas, recomendamos considerar tres aspectos principales para organizar el curso de forma armónica:
Procesos generales
El aprendizaje, tales como el razonamiento; resolver y plantear problemas; La comunicación; modelado y desarrollo, comparación y ejercitaciòn de procedimientos.
Sin seguir la clasificación exclusiva, los procesos que existen en todas las actividades matemáticas se relacionan con lo siguiente:
La elaboración, comparación y ejercitaciòn de procedimientos
Debe realizar cálculos correctamente, seguir instrucciones, realizar cálculos, convertir expresiones algebraicas de una forma a otra, y medir correctamente longitud, área, volumen, etc .; en otras palabras, realizan tareas matemáticas, donde Implica dominar el proceso rutinario que se puede desarrollar de acuerdo con una rutina ordenada. Los procedimientos de aprendizaje o métodos de "saber hacer" en el curso son muy importantes porque ayudan a la aplicación de las matemáticas en la vida diaria.
La modelaciòn
Siempre combine la resolución de problemas extensa con aplicaciones y modelado. La forma de describir la relación entre este juego o el mundo real y las matemáticas es la modelación. El punto de partida para la modelación es una situación de problema real. Treffers y Goffree describen la modelación como “una actividad estructurante y organizadora, mediante la cual el conocimiento y las habilidades adquiridas se utilizan para descubrir regularidades, relaciones y estructuras desconocidas”
La comunicación
La capacidad de comunicarse es la demanda común de todos los seres humanos en todas las actividades, disciplinas, profesiones y lugares de trabajo. Los desafíos planteados por el siglo XXI requieren que todas las personas en ciencia y tecnología tengan las siguientes habilidades:
Producir y presentar argumentos persuasivos y convincentes.
Hacer observaciones y conjeturas, formular preguntas, y reunir y evaluar información.
Construir, interpretar y ligar varias representaciones de ideas y de relaciones.
Comprender, interpretar y evaluar ideas que son presentadas oralmente, por escrito y en forma visual.
Expresar ideas hablando, escribiendo, demostrando y describiendo visualmente de diferentes formas.
El razonamiento
El razonamiento matemático está estrechamente relacionado con las matemáticas (como la comunicación, el modelado y los procesos). En general, entendemos los pensamientos al razonar sobre el orden de los pensamientos para sacar conclusiones. Además, se debe enfatizar que el razonamiento matemático debe existir en el trabajo matemático de todos los estudiantes, por lo que este eje debe estar claramente establecido en todas las actividades matemáticas de los estudiantes.
La resolución y el planteamiento de problemas
Se considera un elemento importante en el desarrollo de la investigación matemática y del conocimiento, se dice que la resolución de problemas debe ser el eje central del currículo matemático, por lo que debe ser parte integral del objetivo principal de la enseñanza y el aprendizaje de las matemáticas.
El contexto
Tiene que ver con los ambientes que rodea el estudiante y que le dan sentido a las matemáticas que aprende.
Conocimientos básicos
Son procesos específicos que desarrollan el pensamiento matemático y con sistemas propios de las matemáticas.
Que son
Pensamiento variacional y sistemas algebraicos y analiticos
Superar la enseñanza de contenidos matemáticos fragmentados y compartidos, para ubicarse en el dominio de un campo conceptual.
Pensamiento aleatorio y los sistemas de datos
Es la integración de la construcción de modelos de fenómenos físicos y el desarrollo de estrategias (como experimentos de simulación y entornos). También se deben comparar y evaluar diferentes soluciones al problema para monitorear posibles conceptos erróneos y declaraciones erróneas.
Pensamientos métricos y sistemas de medida
Promover el desarrollo de capacidades de medición para actividades como: ir al supermercado, cocinar, hacer ejercicio, construir y leer mapas, etc.
Pensamientos especiales y sistemas geométricos
Conjunto de procesos cognitivos a través de los cuales se pueden construir y manipular las representaciones mentales de los objetos espaciales, sus relaciones, sus transformaciones y sus diversas traducciones o representaciones materiales.
Pensamientos numéricos y sistemas numéricos
Los estudiantes tienen la oportunidad de pensar en los números y de usarlos en contextos significativos.
