av Darian Aguirre Lara 4 år siden
167
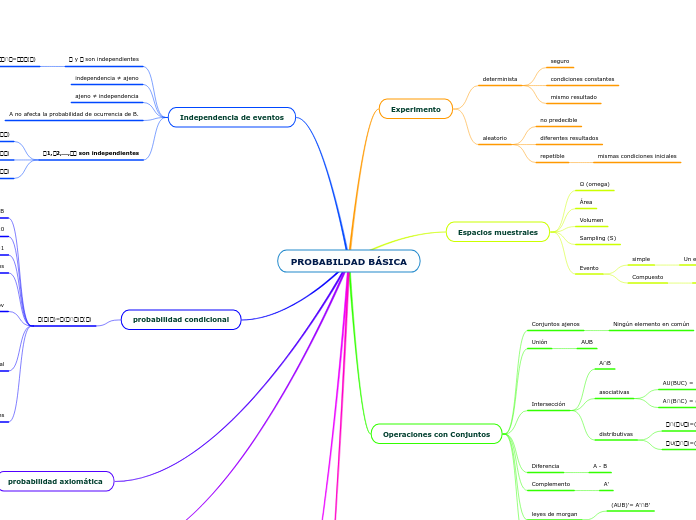
PROBABILDAD BÁSICA
El estudio de la probabilidad básica involucra varios conceptos fundamentales, entre ellos la probabilidad condicional, que se calcula bajo la fórmula de Kolmogorov. Esta fórmula es esencial para determinar la probabilidad de un evento dado otro evento.