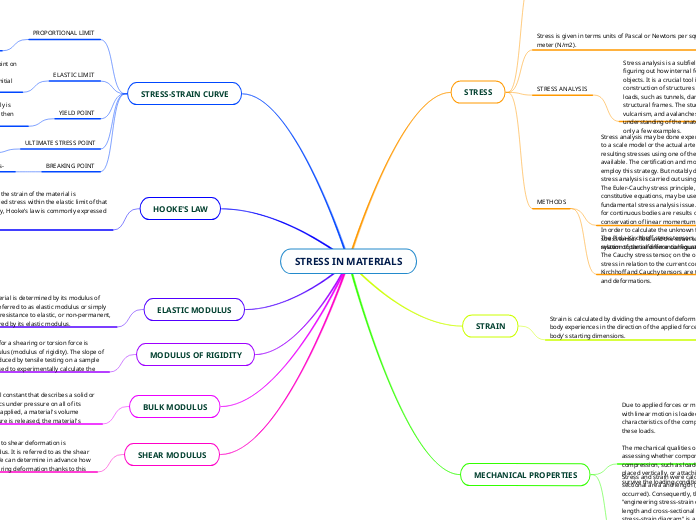
STRESS IN MATERIALS
SHEAR MODULUS
The earth's material reaction to shear deformation is measured by the shear modulus. It is referred to as the shear stress to shear strain ratio. We can determine in advance how resistant a material is to shearing deformation thanks to this useful characteristic.
BULK MODULUS
Bulk modulus is a numerical constant that describes a solid or liquid's elastic characteristics under pressure on all of its surfaces. When pressure is applied, a material's volume decreases; when the pressure is released, the material's volume increases.
MODULUS OF RIGIDITY
The elasticity coefficient for a shearing or torsion force is known as the shear modulus (modulus of rigidity). The slope of a stress-strain curve produced by tensile testing on a sample of the material may be used to experimentally calculate the modulus of rigidity.
ELASTIC MODULUS
The elasticity of a material is determined by its modulus of elasticity, commonly referred to as elastic modulus or simply modulus. A material's resistance to elastic, or non-permanent, deformation is measured by its elastic modulus.
HOOKE'S LAW
Hooke’s Law states that the strain of the material is proportional to the applied stress within the elastic limit of that material. Mathematically, Hooke’s law is commonly expressed as:
F = –k.x
STRESS-STRAIN CURVE
BREAKING POINT
The failure of the material occurs at this point on the stress-strain curve.
ULTIMATE STRESS POINT
It is a point that symbolises the highest stress a material can withstand before failing. Beyond this, failure happens.
YIELD POINT
The point at which a material begins to distort plastically is known as the yield point. The yield point is passed, and then there is permanent plastic deformation.
ELASTIC LIMIT
The material returns to its previous location up to that point on the graph when the load acting on it is totally eliminated. Beyond this point, the material is unable to return to its initial position and begins to exhibit plastic deformation.
PROPORTIONAL LIMIT
It is the part of the stress-strain curve when Hooke's law is followed. The stress-strain ratio provides us with a proportionality constant known as Young's modulus in this limit. The graph's proportional limit is represented by point OA.
MECHANICAL PROPERTIES
Stress and strain were calculated using the initial cross-sectional area and length (before any deformation had occurred). Consequently, the illustration is known as a "engineering stress-strain diagram." However, a material's length and cross-sectional area alter when it deforms. A "true stress-strain diagram" is a stress-strain diagram that calculates stress and strain using the current cross-sectional area and length data.
The engineering stress-strain diagram is adequate for the majority of applications since the discrepancies between the real and engineering versions are minimal below the material's yield point.
Due to applied forces or motion, every component in a system with linear motion is loaded in some way. The mechanical characteristics of the component define how it responds to these loads.
The mechanical qualities of stress and strain are crucial in assessing whether components that are exposed to tension or compression, such as load-bearing balls and rollers, shafts placed vertically, or attaching and joining hardware, can survive the loading conditions of the application.
STRAIN
Strain is calculated by dividing the amount of deformation the body experiences in the direction of the applied force by the body's starting dimensions.
SHEAR STRAIN
Shear strain is the term used to describe the angle tilt that occurs in the body when tangential stress is produced.
VOLUMETRIC STRAIN
Volumetric strain is the strain that results in the body when the deforming force only causes a change in volume.
LONGITUDINAL STRAIN
The strain created in the body is known as longitudinal strain or tensile strain if the deforming force only results in a change in length.
STRESS
METHODS
The Piola-Kirchhoff stress tensors represent the stress in relation to the reference configuration for finite deformations. The Cauchy stress tensor, on the other hand, represents the stress in relation to the current configuration. The Piola-Kirchhoff and Cauchy tensors are the same for tiny rotations and deformations.
Stress analysis may be done experimentally by applying loads to a scale model or the actual artefact and measuring the resulting stresses using one of the many methods that are available. The certification and monitoring of safety frequently employ this strategy. But notably during design, the majority of stress analysis is carried out using mathematical techniques. The Euler-Cauchy stress principle, along with the necessary constitutive equations, may be used to describe the fundamental stress analysis issue. These equations of motion for continuous bodies are results of Newton's principles for the conservation of linear momentum and rotational momentum. In order to calculate the unknown functions that make up the stress tensor field and the strain tensor field, one gets a system of partial differential equations.
STRESS ANALYSIS
Stress analysis is a subfield of applied physics that deals with figuring out how internal forces are distributed within solid objects. It is a crucial tool in engineering for the analysis and construction of structures under predetermined or anticipated loads, such as tunnels, dams, mechanical components, and structural frames. The study of events like plate tectonics, vulcanism, and avalanches in geology, as well as the understanding of the anatomy of living things in biology, are only a few examples.
Typically, structures and things that may be considered to be in macroscopic static equilibrium are the focus of stress analysis. According to Newton's principles of motion, all applied external forces must be counterbalanced by internal reaction forces. These internal reaction forces are nearly invariably surface contact forces between nearby particles, or stress. Because each particle must be in equilibrium, this response stress often spreads from particle to particle, causing a stress distribution throughout the body.
Stress is given in terms units of Pascal or Newtons per square meter (N/m2).
Stress may be defined as the normalised weight exerted over a material or the internal pressure of solid materials.
TENSILE STRESS
The amount of force F applied along an elastic rod divided by the cross-sectional area A of the rod in a direction perpendicular to the applied force is known as tensile stress.
COMPRESSIVE STRESS
Compressive stress is the driving force behind a material's deformation, which results in a decrease in volume. A material's exposure to stress is what causes it to have a lower volume. High compressive stress causes the material to fail because of tension.
SHEER STRESS
The component of stress that is coplanar with a material cross section is known as shear stress and is frequently represented by the Greek letter tau. It results from the shear force, which is the part of the force vector that is parallel to the cross section of the material.