Características Físicas
Si el material utilizado para el núcleo tiene alta permeabilidad, más será la inductancia de un inductor
Cuando se enrolla el cable en una bobina, el campo se hace más fuerte
Se usa comúnmente, el aluminio como material conductor
Existen inductores con núcleo de aire o con núcleo hecho de material ferroso
Formado de espiras de cable, el campo magnético circula por el centro del inductor y cierra su camino por su parte exterior
Si el área de las placas que están frente a frente es grande la capacitancia aumenta
Las placas suelen estar separadas por un aislante llamado “Dieléctrico”
La construcción axial se basa en capas alternas de láminas metálicas y dieléctricas
Si la separación entre placas aumenta, disminuye la capacitancia
Compuesto de dos placas paralelas, una con carga negativa y justo en frente una de igual tamaño pero con carga opuesta
CIRCUITOS RC, RL
ANÁLISIS RESPUESTA
RL
Para lograr que el circuito RL haga algo, necesitamos que un ayudante externo le añada algo de energía y luego se retire y lo deje en paz mientras observamos qué ocurre.
What does it consist of?
fresh papaya, yogurt, whole milk, honey, cardamomuncooked rice, cinnamon bars, water, almonds, coconut juice, sugar, lime, ice, mint leavesdried boba tapioca pearls, water, sugar, almond milk, fruit juiceiced coffee, horchata, sugarmatcha powder, honey, milk, riceOther
Podemos obtener el voltaje por medio de la ley de Ohm:
V(t) = (R)(i(t))
Podemos escribir la ley de voltaje de Kirchhoff comenzando en la esquina superior izquierda del esquema y recorriéndolo en el sentido opuesto a las manecillas del reloj: VL + VR = 0. L (di/dt) + iR=0
2
La corriente en el resistor acaba de brincar de 0 a I0 por lo que el voltaje cambia instantáneamente a v(0^+)= I0R
Dijimos anteriormente que I0 fluye por el inductor justo después de abrirlo. ¿Qué le ocurre al voltaje?
6.
E intentamos con una función exponencial con parámetros ajustables, K y s.
i(t)=Ke^st
Para resolver la ecuación, soñamos con una función para la corriente y la sustituimos en la ecuación diferencial para ver si es correcta.
L(di/dt) + iR =0
5.
Para describir el inductor, usamos su ecuación i-v:L( di/dt)
Para describir el resistor, usamos la ley de Ohm:
vR=IR
4.
La corriente en el inductor es I0 para todo el tiempo anterior a t=0^+t=0.
3.
La corriente en el inductor no cambia instantáneamente (de hecho, le es imposible). Así, la corriente que fluye en el inductor justo después de que abrimos el interruptor es igual a la corriente que fluía cuando estaba cerrado.
2.
Un momento después, en t=0^+ t=0
abrimos el interruptor; la corriente I0 aún fluye por L, y ahora comienza a fluir por R.
1.
En el instante previo a que abra el interruptor, t=0^-t=0
el inductor tiene una corriente que llamaremos I0 y hay 0 volts a través de sus terminales y las del resistor.
RC
En este circuito el capacitor puede cargarse o descargarse.
What does it consist of?
hot cocoa mix, mint chocolate chip ice-cream, fresh mintheavy cream, sugar, nutmeg, eggsnavel orange, apple cider, honey, berries, whole cloves, ground nutmeg, ginger, cinnamon stickscardamom seeds, cloves, black peppercorn, cinnamon sticks, ginger, milk, black tea, sugarvanilla soy milk, espresso, canned pumpkin, cinnamon, cayenne, agave syrup, saltOther
VOLTAJE
El voltaje del capacitor esta dado por Vc =Voe^-t/Rc
Despues de un tiempo T=RC
Esta en función del tiempo esta dada por V=Vo(1-e^t/RC)
El voltaje se incrementas con el tiempo
CORRIENTE
i=dq/dt
Ahora ,¿Cuánto valdría la intensidad de la corriente si el capacitor aún no se a cargado por completo? Este momento es conocido como Regimen transitorio.
Cuando t>0 es decir este cargado la corriente se convierte en 0 , despues de que el capacitor se cargue completamente. En estos ambos casos volveremos a utilizar las leyes de Kirchhoff .
Como dijimos , la corriente varia con el tiempo , entonces cuando este es 0 , la corriente será I=V/R
El instante justo en el cierra el interruptor t=0 significa que el capacitor esta descargado , t>0 despues de cerrar el interruptor el capacitor empieza a cargarse ya que hay una corriente.
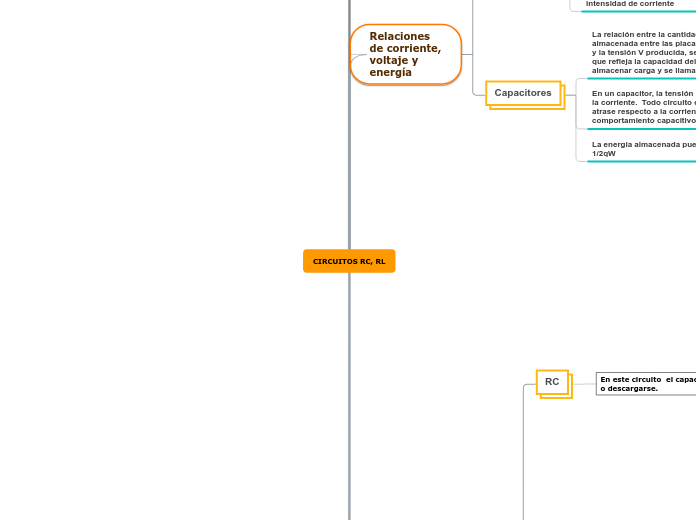
Relaciones de corriente, voltaje y energía
Capacitores
La energía almacenada puede calcularse= 1/2qW
En un capacitor, la tensión atrasa 90º respecto a la corriente. Todo circuito en el cual la tensión atrase respecto a la corriente, se dice que tiene comportamiento capacitivo.
La relación entre la cantidad de carga Q almacenada entre las placas de un capacitor y la tensión V producida, será una constante que refleja la capacidad del capacitor para almacenar carga y se llama capacidad C.
Inductores
La bobina almacena energía en forma de campo magnético cuando aumenta la intensidad de corriente
Voltaje a través del inductor es proporcional al cambio en la corriente que pasa por este.
Identificación de circuitos
Circuito RL
Es un circuito que contiene una resistencia y bobina en serie.
Se tiene una resistencia y bobina en serie.
La corriente en ambos elementos es la misma.
El valor del voltaje es el mismo para
la resistencia y para la bobina.
V=VR=VL
Circuito RC
Es un circuito que esta formado por resistencias
y condensadores. Su forma más simple es de primer orden
compuesto por una resistencia y un condensador.
Serie
La corriente que pasa por el resistor
y por el capacitor es la misma.
Paralelo
La tensión o voltaje es la misma
en el condensador y resistencia;
la corriente se divide entre la resistencia
y el condensador