por JUAN CARLOS ROMERO SANTOS 3 anos atrás
365
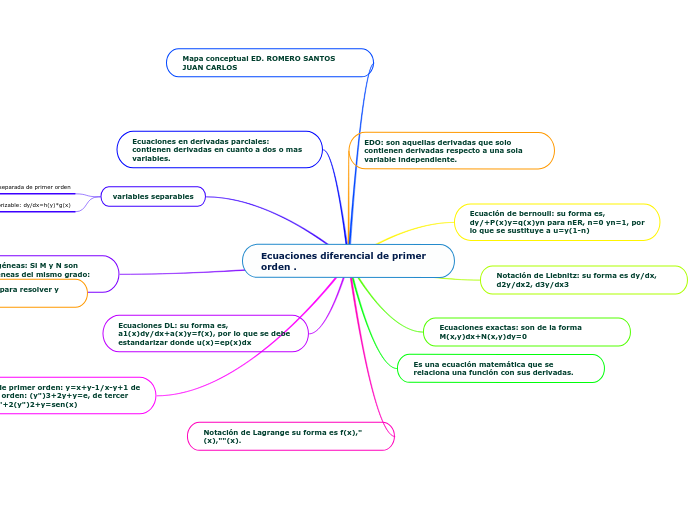
Ecuaciones diferencial de primer orden .
Las ecuaciones diferenciales de primer orden son aquellas que involucran derivadas respecto a una sola variable independiente. Entre las más comunes se encuentran las ecuaciones de Bernoulli, que se pueden transformar mediante una sustitución específica, y las ecuaciones lineales, que requieren una estandarización para su resolución.