por Javiera Rojo 3 anos atrás
308
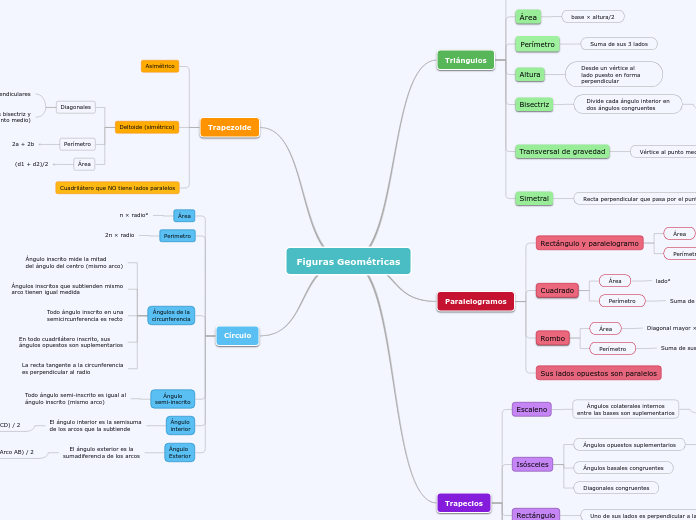
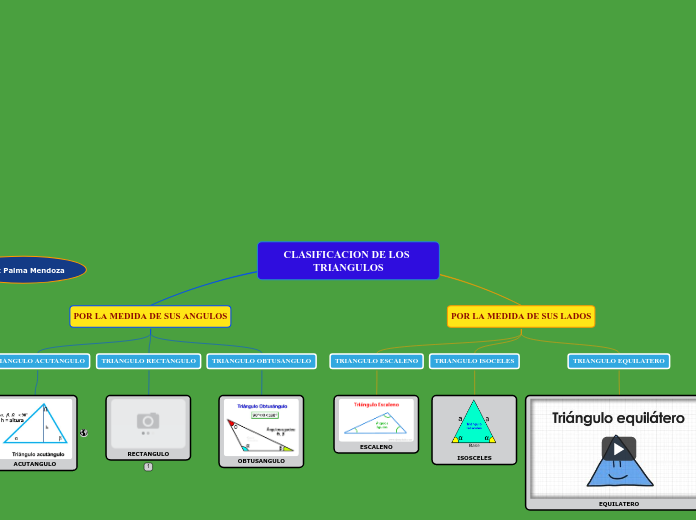
Figuras Geométricas
La geometría abarca diversas figuras, cada una con propiedades específicas en términos de área y perímetro. Los paralelogramos, como el cuadrado y el rombo, tienen fórmulas particulares para calcular estas dimensiones.