Fundamentals of Geometry for Elementary School Teachers
Shapes
Polyhedra
A three - dimensional figure made up of sides called faces, each face being a polygon (polygonal regions).
Other Parts of a Polyhedra:
Vertices then corners, or where the lines/rays/edges meet
Edges the sides of each polygon
Vertex
"The commen point of two or more rays or line segments."
"The ultimate high or low point of two intersecting lines."
Real Life Examples:
The bottom of the letter U
The bottom of the letter V in Vertex
The base of a hand-held fan
*Plural Word: "Vertices"
Ray
"A line that starts at a point with given coordinates, and goes off in a particular direction to infinity, possiably through a second point." ("Ray Definition (Coordinate Geometry) - Math Open Reference." Ray Definition (Coordinate Geometry) - Math Open Reference. N.p., n.d. Web)
"A straight line that begins, but never ends."
Real Life Example:
Sun rays
Line Segment
"A straight line which links two points without extending beyond them." ("Line Segment Definition - Math Open Reference." Line Segment Definition - Math Open Reference.)
"A straight line that begins and ends."
Real Life Examples:
One side of a door frame
One side of a ruler
One side of your TV
Names of Different Polyhedras
Cylinders
At what angle does the line segment between the center of the top base and the center of the bottoem base meet?
Two closed, parallel, curved bases
(often circular, always congruent)
Cones
At what angle does the line segment between the apex and the center of the base meet?
Closed, "Curved" base
(often circular)
Prism
Two congruent polygons, which are parallel planes (called bases), and the lateral faces joining the bases, which are parallelograms.
Ask yourself these three questions:
1.) Is is convex or concave (nonconvex)?
2.) Is it "right" or "oblique"? At what angles do the faces meet the base?
-If the faces are rectangles and they meet at a 90 degree angle, then the prism is called RIGHT.
-Otherwise, it is called OBLIQUE
*Another way to think of this question: Is the pyramid slanted/tilted or straight? If it is straight, it is RIGHT. If it is slanted, it is OBLIQUE.
3.) What polygon is the base?
Example: A nonconvex, right, pentigonal prism.
Lateral
"A side part of something"
Example: The roots of a plant are lateral
Planes
Convex or Concave
Pyramid
Always Convex
Determining Their Names
Ask yourself two questions:
1.) Is is "right" or "oblique"?
-It is RIGHT if you drew a line segment from the apex to the center of the base and this created a 90 degree angle.
-Otherwise, it is OBLIQUE
*Another way to think of this question: Is the pyramid slanted/tilted or straight? If it is straight, it is RIGHT. If it is slanted, it is OBLIQUE
2.) What polygon is the base?
Example of name: The Egyption Pyramids would be "right, square pyramids."
4 or more faces (n + 1)= faces
("n" being the n-gon of the base)
Also note: There are always 4 or more triangles
Apex
The point at which every triangle arising from the base meets.
Polygons
A polygon is an enclosed shape with three or more sides, all of which are straight.
A polygon can be concave or convex and the lines can cross one another.
It is important to note that a polygon can approach the shape of a circle (with increased sides), but it can never actually become a circle because a polygon cannot have any curved lines.
Real Life Examples:
An arrow
A stop sign
A TV
First aid symbol
A triangle
Names of Polygons
More info...
Heptagon
polygon with seven sides
polygon with six sides
Pentagon
polygon with five sides
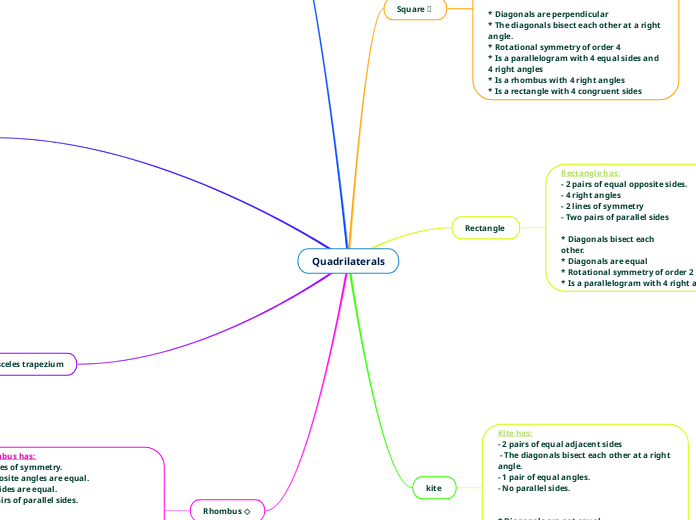
Quadrilaterals (tetragon)
four-sided polygons
Kite
TEXTBOOK DEFINITION: A quadrilateral with two distinct pairs of congruent adjacent sides. A kite can be either convex or concave.
Mathematical Reasoning for Elementary School Teachers. N.p.: Addison-Wesley, 2011. Print.
Parallelograms
TEXTBOOK DEFINITION: A quadrilateral in which each pair of opposite sides is parallel.
Mathematical Reasoning for Elementary School Teachers. N.p.: Addison-Wesley, 2011. Print.
Trapezoid
TEXTBOOK DEFINITION: a quadrilateral with at least on pair of parrellel sides.
Note: Some dictionaries and text require a trapezoid to have exactly one pair of parallel sides
Mathematical Reasoning for Elementary School Teachers. N.p.: Addison-Wesley, 2011. Print.
Isosceles Trapezoid
TEXTBOOK DEFINITION: A trapezoid with a
Mathematical Reasoning for Elementary School Teachers. N.p.: Addison-Wesley, 2011. Print.
Rhombus
TEXTBOOK DEFINITION: a parallelogram
Mathematical Reasoning for Elementary School Teachers. N.p.: Addison-Wesley, 2011. Print.
Note: An Equiangular Rombus is a Square.
Rectangle
TEXTBOOK DEFINITION: A parallelogram with a right angle.
Mathematical Reasoning for Elementary School Teachers. N.p.: Addison-Wesley, 2011. Print.
A rectangle with all sides of equal length.
Triangles (trigon)
three-sided polygons
Types of Triangles
Scalene
A triangle with no two sides of equal length (no equal angles)
Isoceles
A triangle with two egual sides and two of the same angles.
Equilateral
A triangle with all equal sides/angles.
A triangle with a right angle within it.
A triangle with and obtuse angle within it.
A triangle that has all acute angles within.
The sum of all of the angles within a triangle is 180 degrees.
Formula for the Sum of the Angles Within ANY Polygon
Take the number of sides the polygon has and minus two. Then multiply this number by 180 degrees.
OR
Take the number of sides the polygon has and multiply it by 180, then subtract 360 from the total.
Lattice Polygon
"Formed by a rubber band stretched over the nails of a geoboard."
Long, Calvin T., and Duane W. DeTemple. Mathematical Reasoning for Elemertary Teachers. Reading, MA: Addison-Wesley, 2000. Print.
Self-itersecting Polygon
Where the lines of a polygon intersect one another.
Convex
Concave
Equilateral Polygon
All sides are congruent (same).
Congruent
"Equal in size or shape."
Real Life Examples:
Two of the same mugs
Identical twins
The squares on a calendar
Equiangluar Polygon
All angles are congruent (same)
Regular Polygon
A convex polygon, both equilateral and equiangular.
When a polygon has an odd number of sides....
If it is equilagular it has to be equilateral aswell,
and vise versa.
Why?
Because it has no parallel sides.
Tiling and Tessellations
Semi-regular Tiling
Using more then one regular polygon to make 360 degrees at the vertex.
Same pattern at every vertex
Regular Tiling
Definitions/ ways to think about it:
1.) "Using only one polygon to make 360 degrees at the vertex."
2.) "Does to vertex of one polygon add up to 360 degrees?"/"Can the interior angle of the polygon be multiplied to equal 360 degrees?" If yes, then the tessellation is regular.
3.) "The angles that meet at the vertex (using only one polygon) add up to 360."
Only 3 Regular Tilings:
Hexagon
Square
Triangle
Help on Geometers Sketchpad
Transformations
Chapter 11
Glide
reflection (glide-flip)
Reflection
flip
Rotation
turn from a given point
COUNTERCLOCKWISE
Translation
slide
Angles
"The space measured between two intersecting lines."
Real Life Examples:
Peice of wood cut at a 15 degree angle to make a stool for your kitchen
Corner of a room
The angle between the two intersecting cuts of one slice of pizza
The corner of a brownie
The corner of my book/paper
Describing Angles in Relation to Their Degree
Reflex
An angle that is greater than 180 degrees, but less then 360. Often refered to in Layman's terms as the "outside" angle.
Straight
An angle that lies on a straight line. This angle can also be measured as 180 degrees.
Obtuse
An angle greater then 90 degrees, but less then 180.
Right
An angle of 90 degrees, where two intersecting lines are perpendicular to one another.
Perpendicular Lines
"A line that meets or crosses another line at right angles (90 degrees)."
"Two lines that have opposite (negative reciprocal) slopes."
Real Life Examples:
A cross
The lower case letter " t "
The sign people make with their arms when they call for a "timeout"
Negative Reciprocal
Acute
An angle greater then zero degrees and less then 90 degrees.
Zero
An angle of zero degrees where two lines lay on top of one another.
Parallel Lines
"Two lines on a plane that never meet and they are always the same distance apart because they have the same slope."
Real life examples:
Monkey Bars
Street yellow lines (when road is straight)
Rail road tracks
The L's in the word parallel
Supplementary Angles
"Sum of two angels is 180 degrees."
Real Life Examples:
Freeway entrance
My leg standing on top of the floor
Two slices of pizza from a pizza cut into fours
The letter t
Trick for Memorization:
"S" for straight
Complementary Angles
"Sum of two angels is 90 degrees."
Real Life Examples:
Park bench (two 45 degree angles)
Sandwhich (sliced from one corner to any other end of the sandwhich)
Two peices of pizza (from a full pizza cut into eight slices)
Trick for Memorization:
"C" for corner
Vertical Angles
Corresponding Angles
Regular Polygon Angles
Exterior Angle
Central Angle
360/n
Interior Angle
(n-2)180/n OR 180-(360/n)