por lizara vallelado 3 anos atrás
295
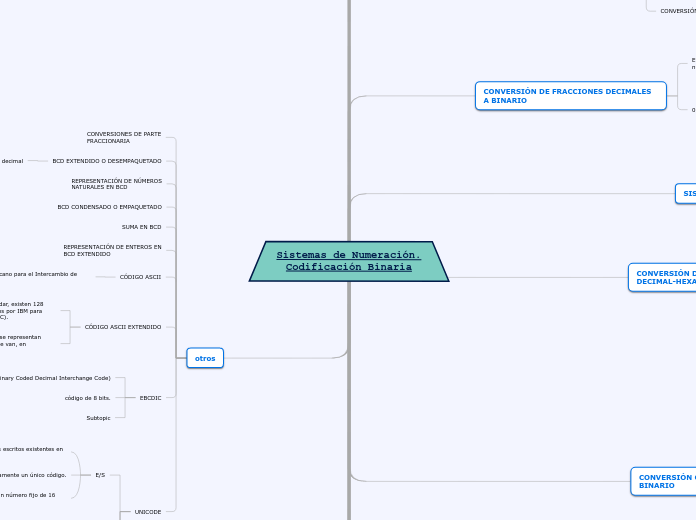
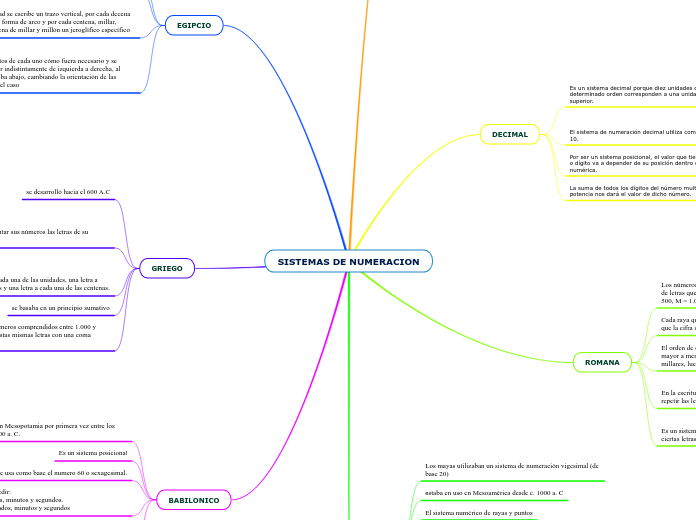
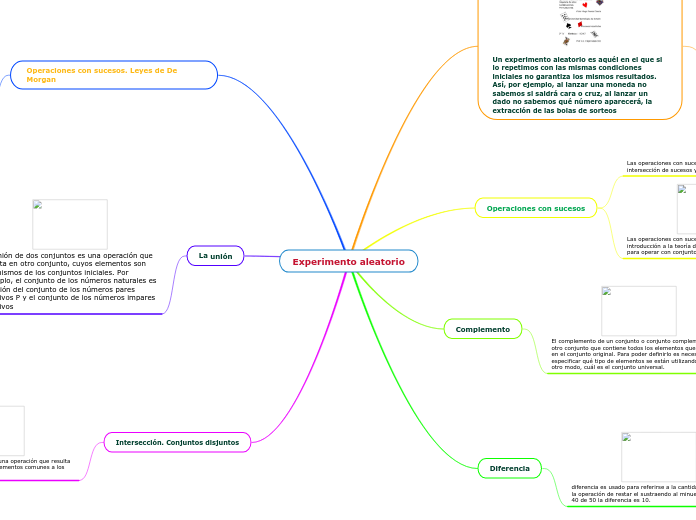
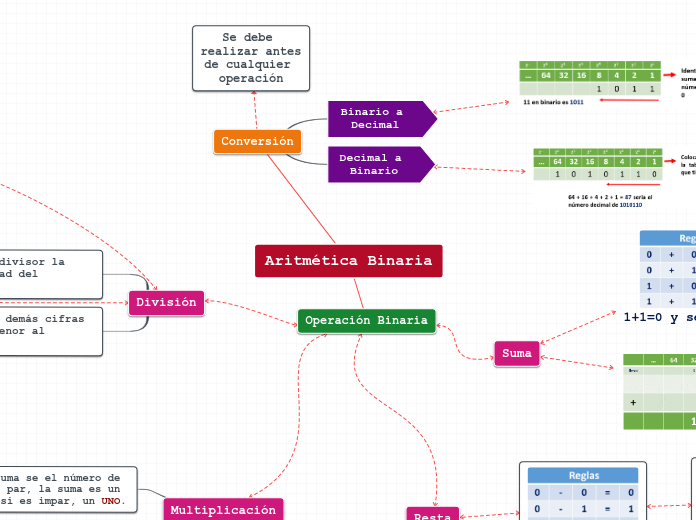
Organigrama arbol
Los sistemas de numeración son esenciales para representar y manipular números en diversos formatos. El sistema decimal, uno de los más conocidos, se basa en diez dígitos del 0 al 9, donde la posición de cada dígito determina su peso, que es una potencia de diez.