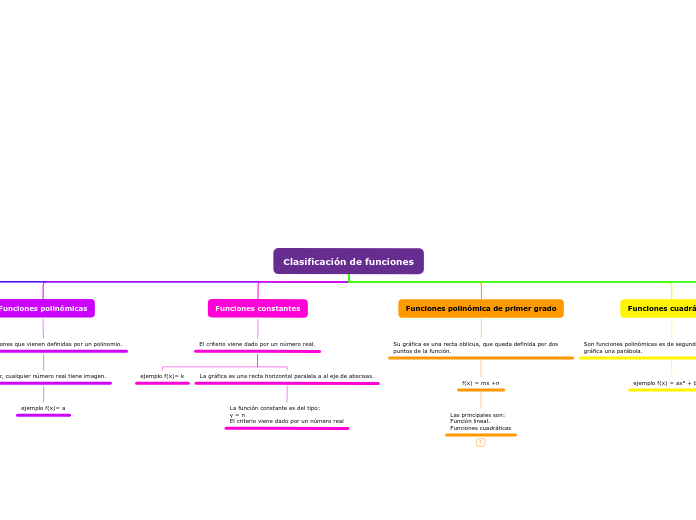
Clasificación de funciones
Funciones racionales
El criterio viene dado por un cociente entre polinomios: f (x ) = 1 / x – 2, el dominio es toda x excepto x =2.
El dominio lo forman todos los números reales excepto los valores de x que anulan
el denominador.
Función exponencial.
Sea a un número real positivo. La función que a cada número real x le hace
corresponder la potencia ax se llama función exponencial de base a y exponente x.
Un ejemplo de una función exponencial es el crecimiento de las bacterias. Algunas bacterias se duplican cada hora. Si comienzas con 1 bacteria y se duplica en cada hora, tendrás 2x bacterias después de x horas.
Funciones trascendentes
tiene variable independiente figura como exponente
o se
halla afectada del signo logaritmo o de cualquiera de los signos que emplea la
trigonometría.
Funciones cuadráticas
Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.
ejemplo f(x) = ax² + bx +c
Funciones polinómica de primer grado
Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.
f(x) = mx +n
Las principales son:
Función lineal.
Funciones cuadráticas
Funciones constantes
El criterio viene dado por un número real.
La gráfica es una recta horizontal paralela a al eje de abscisas.
La función constante es del tipo:
y = n
El criterio viene dado por un número real
ejemplo f(x)= k
Funciones polinómicas
Son las funciones que vienen definidas por un polinomio.
es decir, cualquier número real tiene imagen.
ejemplo f(x)= a
Funciones implícitas
llamada función implícita, si la variable dependiente no se produce de forma explícita, en un lado de la ecuación,
ejemplo 5x − y − 2 = 0
Funciones explícitas
Si se pueden obtener las imágenes de x por simple sustitución.
f(x) = 5x − 2
ejemplo f(x) = 5x − 2
Funciones algebraicas
hay que efectuar con la
variable independiente son: la adición, sustracción, multiplicación, división,
potenciación y radicación.
Subtopic