Parábolas

Mais informações

FIGURAS CONICAS- CARLOS JAVIER LEÓN ESPINOZA

por Carlos Javier Leon Espinoza

La tradicion oral.

por jfamcas jfamcas

Movimiento rectilíneo uniformemente acelerado

por Aida Torres

Parabola y Circunferencia

por Alejandro Reyes

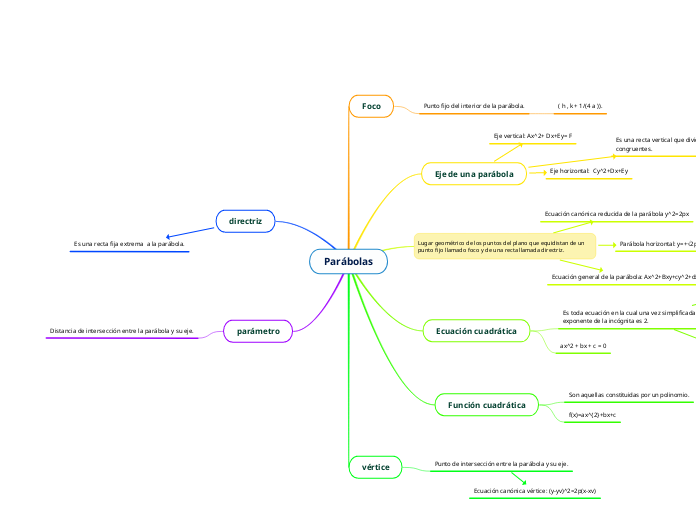
Parábolas

parámetro

Distancia de intersección entre la parábola y su eje.

directriz

Es una recta fija extrema a la parábola.

vértice

Punto de intersección entre la parábola y su eje.

Ecuación canónica vértice: (y-yv)^2=2p(x-xv)

Función cuadrática

f(x)=ax^{2}+bx+c

Son aquellas constituidas por un polinomio.

Ecuación cuadrática

ax^2 + bx + c = 0

Es toda ecuación en la cual una vez simplificada el mayor exponente de la incógnita es 2.

Resolución de ecuaciones cuadráticas

Es hallar las raíces de la ecuación. Para ello hacemos uso de la fórmula: x = [ – b ± √(b2 – 4ac) ] / 2a

Ecuaciones cuadráticas incompletas

Son ecuaciones de la forma ax2 + c = 0 que carecen del término x o de la forma ax2 + bx = 0 que carecen del término independiente.

Ecuaciones cuadráticas completas

Son ecuaciones de la forma ax2 + bx + c = 0 que tienen un término x2, un término x y un término independiente de x.

Lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta llamada directriz.

Ecuación general de la parábola: Ax^2+Bxy+cy^2+dx+ey=f

Parábola horizontal: y=+√2px, Y=-√2px

Ecuación canónica reducida de la parábola y^2=2px

Eje de una parábola

Eje horizontal: Cy^2+Dx+Ey

Eje vertical: Ax^2+ Dx+Ey= F

Es una recta vertical que divide la parábola en dos mitades congruentes.

Foco

Punto fijo del interior de la parábola.

( h , k + 1/(4 a )).