realizată de Gauthier Samuel 8 ani în urmă
234
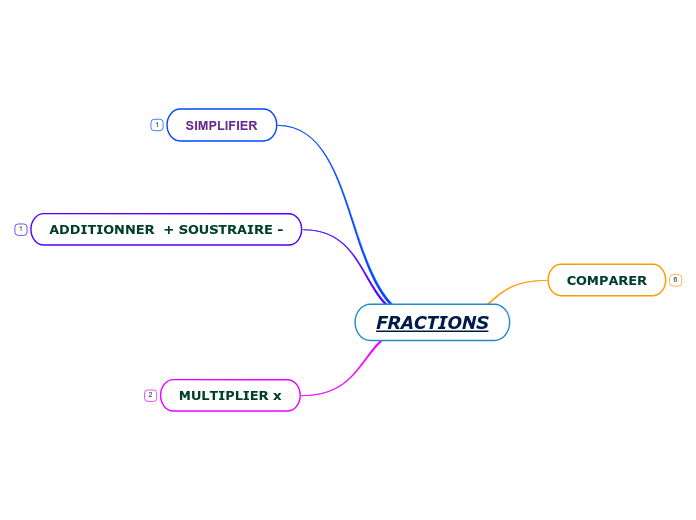
Parcours personnalisé pédagogie de projet et pédagogie active - Maths
L'enseignement des fractions peut être abordé de manière innovante en utilisant une définition minimaliste où le numérateur et le dénominateur sont séparés par une barre centrale. Les fractions peuvent être simplifiées en identifiant celles équivalentes à l'